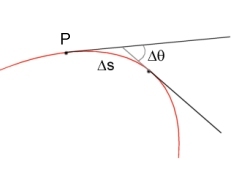
 Let's imagine a generic line drawn on a plane. The curvature, as suggested by the intuition, is the measure of its deviation from the straightness. The straightness is defined by the tangent line.
Let's imagine a generic line drawn on a plane. The curvature, as suggested by the intuition, is the measure of its deviation from the straightness. The straightness is defined by the tangent line.
Besides, it is easy to find that curvature is a local property, not a global one.
In other words, it is meaningful to define the curvature for a single point, but it's meaningless to talk about "the curvature of a line".
The curvature in a point P is calculated as follows
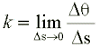 (1)
(1)
It is easy to verify that a straight line has curvature zero. Let's imagine now the simplest curved line: the circle. Its curvature is the same for all the points and its value is k=1/R. The bigger is the radius, the smaller is the curvature. If we consider the straight line as a circle whose radius is infinite, we find again that its curvature is zero. This is consistent with our previous thought.
To measure the curvature k we should calculate a limit, but we know that often this is a not-so-easy calculation.
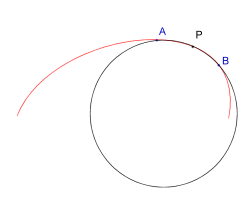
Happily, it exists an esplicit formula that can provide the radius of curvature. Let's consider three points on a curved line: A, B and the middle point P. A and B can slide symmetrically approaching P between them. The distance between A and B is ![]() .
.
We can easily build the circle passing for those three points: it will be a good approximation of the curve as long as ![]() goes to zero. Knowing the circle's radius, we immediately get the curvature of the line around P: it's again k=1/R.
goes to zero. Knowing the circle's radius, we immediately get the curvature of the line around P: it's again k=1/R.
It is easy to find that circle: it's nothing that the osculating circle. The name derives from Circulum osculans because it "kisses" the line around the point P (osculum = kiss). Its formula requires the first and second derivative of the line in a cartesian coordinate system.
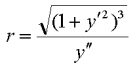 (2)
(2)
It is true that the radius is a geometrical entity, so it is always positive, but we can interpret a negative value for curvature as a concavity directed bottomwise with respect to our cartesian coordinate system.
Herewith we show some examples that the students can verify themselves studying the functions.
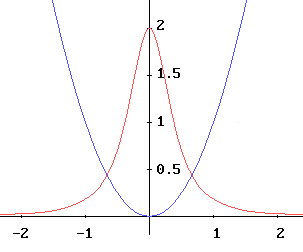
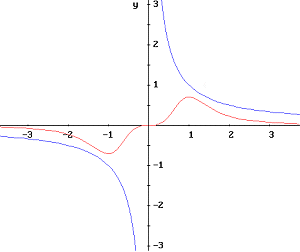
Left: plotted in blue the parabola y=x², right the hyperbola y=1/x. In red are shown their curvatures.
It should be noted that the sign of the curvature in the hyperbola reflects the direction of its concavity.
 2-D: the curvature of a surface
2-D: the curvature of a surfaceLet's proceed with our study of the curvature by considering a regular surface. We will talk about the gaussian curvature, so named in honor of the great mathematician Carl Friedrich Gauss, who gave its description.
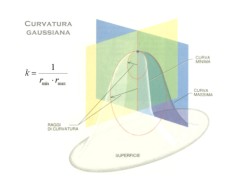
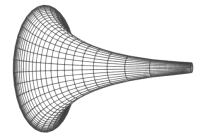
Let's consider the flattened bell shown beside: to find the curvature at the apex, first we have to find the line perpendicular to the surface. Then, we shall consider the set of planes passing for that line. They will cut the bell defining different curves.
There is a theorem, due to Euler, asserting that the curves with maximum and minimum curvature lie in perpendicular planes. Thus, we have to find those planes and measure the radius of the osculating circles. Gauss defined the (gaussian) curvature as the product of those curvatures.
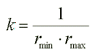 (3)
(3)
If we consider a point P on a sphere of radius R, it is easy to think that all the planes passing by the perpendicular cuts the sphere defining equal curves (circles of radius R). The gaussian curvature of the sphere is then 1/R² for all the points. The sphere is a surface with constant positive curvature.
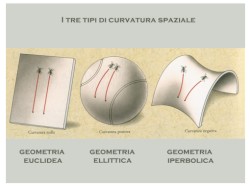 The three kinds of curvature
The three kinds of curvatureRecalling the fact that the curvature has a sign, it follows that the product (3) of two curvatures could be positive, negative, or zero. It depends upon the fact that the osculating circles lies in the same side with respect to the surface or in opposite sides.
Question: how is the curvature of a cylinder? and that of the cone?
The intuition in this case doesn't help us! Those surfaces are not curved! In fact for every point of the cylinder or the cone we can find a plane that cuts the figures finding a minimum curvature line: a straight line.
Since the gaussian curvature is a product and one of the factors is zero, the result too will be zero. Cylinder and cone are flat figures: indeed they can be unrolled and flattened perfectly on the plane.
Gauss found that the surfaces with an intrinsecal curvature are just three: the plane (k=0), the sphere (k=1) and the pseudosphere(1) (k=-1). Intrinsecal curvature means that all the points of those surfaces are equivalent: they have the same curvature. The hypotetical inhabitants of those "worlds" would be able to discover geometric laws, becaus their space is homogeneous. On the contrary, the inhabitants of worlds with non-homogeneous space would experiment strange effects: the geometric figures would change by changing their position.
In 1854 Riemann established the relationship between the kind of geometry and curvature: it is euclidean if the curvature is zero, it is spherical if the curvature is positive and hyperbolic if the curvature is negative.
Question: do the surfaces with curvature ±2 or ±3 have an intrinsic geometry, as long as those of curvature ±1?
Yes, they have, the true distinction don't lie in the absolute value of the curvature. The really important thing is the fact that the curvature is the same for all the points.Question: do the constant curvature have a relationship with the space's homogeneity? and with isotropy too?
Yes, as we said earlier, if the curvature wasn't the same for all the points, the geometric figures would experiment deformations following simple translations. That means that the points of the space would be not equivalent each other: the space would not be homogeneous.
The isotropy is a consequence of the fact that the principal curvatures are equal in absolute value. A curved space whose curvature is 1 because the principal curvatures are 1/2 and 2 is not an isotropic space. The pseudosphere shown at right is a homogeneous space but is not isotropic: for all the points the principal curvatures are variable, holding their product equal to -1.
From a physical point of view, in astronomy the cosmological principle has a happy consequence: the space is homogeneous and isotropic. This greatly simplifies cosmology because we can consider just three possibilities for the geometry of the universe as a whole: flat, spherical and hyperbolical.
On surfaces having constant and positive curvature is defined a spherical geometry, whose main properties are:
- straight lines are great circles
- is not possible to find a parallel straight line passing for a point P external to another straight line: they always intersect
- the sum of internal angles of a triangle is greater than p
radians
- given a circle, the ratio between its circumference and radius is smaller than 2p
- the surface's extension is finite
Question: the Earth's curvature is positive, so on its surface we can define a spherical geometry. I know that parallels never meet, so one of the above mentioned properties is false. Isn't it?
No, because you have to recall the first property. Under the perspective of the spherical geometry, parallels on the Earth's surface are not straight lines! Straight lines are great circles, that means circles whose center coincides with the sphere's center. Of course, great circles always intersect (in two opposite points).
 The hyperbolic geometry
The hyperbolic geometryOn surfaces with constant negative curvature can be defined an hyperbolic geometry, whose main properties are:
- for a point P external to a straight line it is possible to draw infinite parallel straight lines
- the sum of internal angles of a triangle is smaller than p radians
- given a circle, the ratio between its circumference and radius is larger than 2p
- the surface's extension is infinite
It seems impossible to represent the pseudosphere in a portion of a plane, because of its infiniteness. Actually there exists more than one representation. The most interesting is the Poincaré hyperbolic disk because is conformal, so that retains angles and geometrical figures' shape.
The famous artist M. C. Escher made four works using the Poincaré's representation of the hyperbolical space. We can see above Circle limit IV (1960), better known as Heaven and hell. In the hyperbolical geometry all the figures have the same extension but projecting them in the ordinary flat plane they collect at the circle's limit.
To study the properties of hyperbolic geometry, the Mathematics department of Rice University made a beautiful Java applet called NonEuclid. We recommend it greatly.
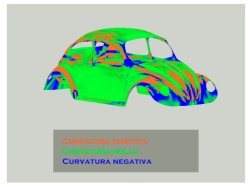 Intermezzo: the famous VW beetle
Intermezzo: the famous VW beetleAs a nice example, we show here a graphical elaboration of the chassis of the old loved Volkswagen Beetle. The colors represents the surface's curvature. One should recall that where the curvature is negative (blue) the osculating circles lie in opposite sides with respect to the surface.
It should be noted also that the top is not curved, is just bended: its geometry indeed is flat.
For sake of completeness, we say that a point where the curvature is positive is called elliptic, where the curvature is negative is hyperbolic, if the curvature is zero but one of the two principal curvature is not zero we are dealing with parabolic points, if all the two curvatures are zero the points are planar.
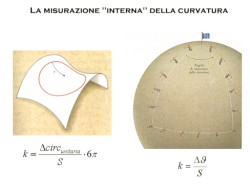 Gauss' theorema egregium
Gauss' theorema egregiumSo far, we considered only lines and surfaces immersed respectively in the plane and in the space.
It's important to point out that to be able to measure their curvature we had to add one dimension!
Gauss discovered that curvature is an intrinsic property, that means it can be measured "remaining inside", without calling for further dimensions.
Gauss was a very exhigent mathematician: he discovered also the hyperbolic geometry but he did not publish this discovery, to avoid the kantian philosophers' objections(2). This time the result was so important that himself called it theorema egregium (eminent theorem).
Let's see three ways to measure the surface's curvature "from inside":
1 - the flowerbed
The inhabitants
of a sphere (as we are, after all!) could use a string to trace a circle on the ground (as gardeners do), measure the length of the circumference and the radius. For instance, staying at a nort pole holding a string 10.000 km long, we could trace a circle that coincides with the equator (40.000 km long). The problem is that for this circle, the ratio between circumference and radius is not 2p, is 4!
The conclusion is that we deal with a spherical geometry: thus we live on a positively curved surface.
2 - the parallel transport
A man at the north pole has the task to walk towards the equator with a mandatory instruction: he must hold a javelin pointing in the same direction. The man has to move the javelin always parallel to himself. At the equator the man walks again but perpendicularly with respect to the previous direction, then he returns to the north pole closing its path. Surprisingly: he finds that with respect to the javelin's direction at the start, now the javelin has rotated. How it could be, since the man never rotated it? Because the surface enclosed by the path is curved!
 3
- Gauss' mountains
3
- Gauss' mountains
Three men are at the top of three distant mountains. They can see each other and they can measure the angle between the other two. When they met, they find that the sum of the three angles is not p, is bigger!
Historically Gauss is said to have really made this measurement because he was charged to compile the geodetic net for the region around Gottingen, but it is false (see the Gauss' biography of W.K. Buhler, Springer-Verlag, 1981). Gauss was aware that the experimental errors were too big: they would have masked the small systematic deviation from p.
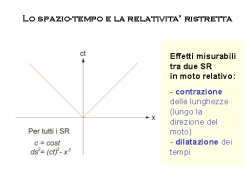 4-D*: the Minkowski's spacetime
4-D*: the Minkowski's spacetimeAfter having dealt with lines and surfaces, now we should talk about the curvature of the space, but we will directly jump to something farther: the spacetime.
With the fundamental article of 1905, Einstein showed that space and time should not be considered anymore absolute quantities. The picture was still confused, when in 1908 the mathematician Hermann Minkowski found the right way to represent the natural scenery for relativity.
The space and the time should not be considered separately, they have to be blended in a single entity called spacetime, whose properties are astounding.
Despite its name, in relativity there are two absolute quantities:
- in every reference system the speed of light is a constant, whose value is 299.792,458 km/s
- in every reference system the spacetime separation between two events (called metric) is constant and it is calculated as ds² = d(ct)² - dx² - dy² - dz².(3)
As a consequence, it's silly to espress the relativity theory with the phrase "everything is relative" !
From the two principles just shown, it can be demonstrated that two observers in relative motion do measure
lenghts and time intervals in a different way. For instance they can measure a length shortening and a time dilation.
Question: do the minus sign in the spacetime metric mean that its curvature is negative?
No, don't confuse the curvature sign with the signs in the metric definition. The picture is quite complicated.
If the signature was (+ + + +) it would just imply that the spacetime would be a riemannian manifold. Its curvature could be either positive, zero or negative. The signature (+ - - -), also called hyperbolic normal, is a property of semi-riemannian manifolds. It has nothing to do with curvature. Instead, the main consequence is that does not exist a minimal length for a line joining two events.
It just exists a line of maximal length, that corresponds to a maximum proper time. In effect, the essence of the inertia's principle in relativity is that bodies move in a way that makes maximum their aging!Question: couldn't we consider the time as an imaginary quantity? This way t² would be equal to -|t²| and the signature of spacetime would be the ordinary (+ + + +)
In effect some calculations in quantum field theory require the analytical prolongation of time from a real coordinate to imaginary (Wick's rotation). Thus the spacetime becomes a riemannian manifold. For instance, the Hartle and Hawking's theory on non-singular origin of the Universe relies on the imaginary time. When the size of the Universe is smaller than 10-43 it is mandatory to use the quantum physics. But things are not so simple: we have to say that there are big difficulties: it is impossible to establish a relationship between the time as a imaginary coordinate with the differential geometry of general relativity. Besides, the Wick's rotation is mathematically well grounded just in flat space. What does it mean in a curved space is still under study.
Hawking is perhaps too unscrupolous when he speaks of the Wick's rotation in the intense gravitational field of black holes.
Last but not least, it should be noted that just the hyperbolic normal metric (+ - - -) allows to distinguish (4), through the ds² sign, events that are in a causal relationship and those causally separated.
Beware: the following three slides are useful to introduce the relationship between curvature and gravity, following a conceptual path developed by Einstein itself. This way to deal the problem can be also found in many textbooks, but it is mathematically ill-grounded! In fact, there not exists a space in rest with the disk, so it's meaningless to ask what kind of geometry exhibits the disk.
Modern textbooks are right to avoid this example. Thanks to dr. Valter Moretti for pointing out that.
Fortunately, this does not falsify the important conclusion that a gravitational field is equivalent to a curved spacetime.
|
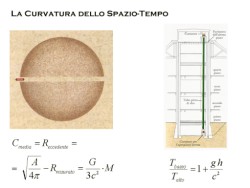 The curvature of the spacetime
The curvature of the spacetimeThe general theory of relativity has shown that the source of the spacetime curvature is the mass-energy. Also in this latter case we have to unify what we previously thought as separate things: the mass and the energy.
We could measure this effect by digging a tunnel through the Sun, if it was a perfect homogeneous sphere and ... colder. From the measure of the surface, we could calculate the solar radius, knowng that S=4pR². By measuring the diameter through the tunnel we could see that there would be a lack of 500 metres! The spacetime curvature has made the euclidean geometry formulas no more valid. For the Earth, whose mass is a fraction of the Sun, this difference would be just about 1,5 millimetres.
So far we discussed about lengths, but the same holds also for time intervals. This effect has been experimentally demonstrated by Pound and Rebka in 1959. They put two identical atomic clocks at the top and at bottom of a 22 m high tower: the time flowed slowly at bottom, because it is immersed in a stronger gravitational field! The curvature is manifesting itself as a slowing of time.
 The geometrodynamics
The geometrodynamicsThe Einstein's theory could be called geometrodynamics because it relates the geometry (of the spacetime) and the dynamics, the study of motion and forces. Gravity, thought by Newton as a force vector, now is regarded as the effect of the spacetime curvature.
The fundamental equation of geometrodynamics, shown beside for mystic's sake, seems very simple. At contrary, it resumes 10 nonlinear tensorial equations!
Einstein himself when he proposed those hard equations did not believe that a solution could be ever found. Surprisingly just one year later, in 1916, the astronomer Karl Schwartzschild showed the unique exact solution of Eistein's equations: the gravitational field outside a non rotating, uncharged body.
The Einstein's masterwork made possible to study black holes, the Universe as a whole and gravitational waves.
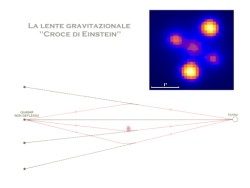 The Einstein cross
The Einstein crossIt's a magnificent demonstration of the bending of light due to a very intense gravitational field. The image seems to show five different objects, actually they are just two!
The object near the field centre is a massive galaxy whose gravitational field distorts the spacetime. The light has no mass: how it should be attracted by a mass? The gravitational field act in a more subtle way: it bends the space(time) thus also the light follows a curved path.
To be simple, also a train cannot steer: it go always straight. But since the railway is bended, the train path is bended too.
The light rays coming from a distant quasar are deflected and made converging towards the Earth, where we see four distant replicas of the quasar.
Again, this curvature affects not only the space but also the time.
A detailed study of the signals coming from the space probes when the Sun is between the Earth and the probe, shows that also time is distorted.
The first attempt to directly measure the curvature of the Universe was made by Edwin Hubble in the thirties of past century. By counting the number of galaxies in spheres of increasing volume, he wanted to test the euclidean nature of the Universe's geometry.
In fact, if we assume that galaxies are uniformally spread througout the Universe, the ratio between counts and 4/3pR³ must be a linear relationship. If it would have been a growing relationship, recalling what we saw in the 2-D case, it would have demonstrated the hyperbolic geometry of cosmos. The opposite for the diminishing counts.
Its conclusions were heavily affected by errors, so he mildly suggested that galaxies grows less than predicted, so the geometry of The Universe could have been positive, with a radius of curvature of about 100 millions of light-years.
Nowadays this method has been abandoned for many reasons: mainly because galaxies that can be easily seen in "small" telescopes are not uniformly spread.
 To measure the Universe's curvature today the astronomers use the theory of relativity. According to Einstein, the curvature of the Universe is completely a consequence of its matter-energy content. This also influences the evolution and the fate of the Universe, as shown in the table.
To measure the Universe's curvature today the astronomers use the theory of relativity. According to Einstein, the curvature of the Universe is completely a consequence of its matter-energy content. This also influences the evolution and the fate of the Universe, as shown in the table.
The main problem is to measure the content of the Universe. If we consider just what is visible, we are forced to say that the Universe contains only the 1% of the amount needed to close the Universe: it will expand forever. Also iIncluding the elusive dark matter we can reach up to 30%.
But there is another method that is giving many surprises: remote supernovas observing.
Supernovas are a class of stars that violently explodes making themselves visible at great distances. We can see supernova even in galaxies distant billions of light-years. Strangely: they appear as 25% dimmer than expected(5).
This can be explained in two ways:
1 - the Universe has a negative curvature. In fact, as for the saddle-shaped surface shown before, the circumference is larger that 2pR, in 3-D the light emitted by the star is spread on a volume larger than 4pR²: this explains why their luminosity is lower than expected.
2 - the Universe is flat but its expansion is accelerating. The distance of the supernovas can be measured through their redshift, but if the Universe is accelerating, the redshift is no longer a trustable indicator. The supernova's distance is then larger, this explains the lower luminosity.
It's a rather complicated situation. After 2003, with the fantastic performance of the WMAP space probe, we know that the geometry of the Universe is flat. This mean that the second explanation is true, but then we are dealing with a mysterious repulsive force that physics cannot explain yet. The scenario is still open: stay tuned for next decades discoveries!
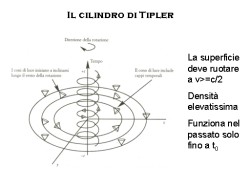 Finale: a "simple" time machine
Finale: a "simple" time machine So far we described the curvature of spacetime as the proper explanation of the gravity, without practical applications. However, a strong spacetime curvature could behave as a time machine. The first scientist who published on a trustable physics journal a description of how to build a time machine was Frank Tipler, in 1974 (Rotating cylinders and the possibility of a global causality
violation, Physical Review D, 9, pp. 2203-2206). In the paper(6) he showed that a cylinder of infinite length (but also a finite length could also works) whose surface rotates at c/2 deformates the spacetime near the cylinder in a way that the time becomes a purely geometric dimension. That means that moving an object in space imply instead a time travel. This way, a right number of turns around the cylinder could bring the time traveller in the past. The maximum reachable is the time in wich the cylinder has been built.
This is of course well over our possibilities, but it's allowed by physics, and this is always the first step.
Notes:
(1) - Usually is called pseudosphere the model of hyperbolic geometry, as long as the sphere is the model of spherical geometry. However, there are some subtilties: a theorem due to Hilbert says that cannot exist models of hyperbolic geometry that can be embedded in the euclidean space and upon wich we can measure distances and angles in the ordinary euclidean way.
 The theorem leaves just four possibilities: the euclidean models of hyperbolic geometry must either
The theorem leaves just four possibilities: the euclidean models of hyperbolic geometry must either
- not to be embeddable in the euclidean space
- to be a partial model
- to change the measure of distances
- to change the measure of angles.
The real pseudosphere (right) is a partial model: it has a hole, but the hyperbolic surface have not.
The Klein-Beltrami model measures angles in a different way with respect to the euclidean one.
The Poincaré model measures distances in a different way.
The most natural model, from wich we can derive all the others with appropriate projections, is the Weierstrass model. It is a hyperboloid of two sheets upon wich we measure distances with the Minkowski's metric.
For instance, the Klein-Beltrami model is obtained by projecting stereographically the hyperboloid onto the point (0,0,0); the Poincaré model is obtained by projecting stereographically the hyperboloid onto the point (0,0,-1);
(2) - The beautiful edification of the euclidean geometry, with the powerful deduction system starting from the five postulates and explains all the properties of geometric figures, inclined Kant and its followers to think that it was logically necessary.
The first person to think that instead the geometry had to receive a confirmation from experience was Gauss. In the book the meaning of relativity Einstein says "I have always been convinced that philosophers have had a negative influence on the development of scientific knowledge because they have subtracted many fundamental concepts from the domain of empirism, in wich they are under our verification, and they have brought them to the unreachable heights of the a priori".
He was referring to the ideas of space and time, but this citation appears adequate to the relationship between geometry and physical reality.
(3) - The distance, in the ordinary euclidean geometry, is expressed throug the Pythagoras' theorem applied to the coordinated. Thus the separation between two points in space is
ds² = dx² + dy² + dz².
We define signature the set of signs of squared coordinates, in this case it is (+ + +).
In the Minkowski spacetime, the separation between two events is expressed as
ds² = d(ct)² - dx² - dy² - dz²
whose signature is (+ - - -) or also as
ds² = dx² + dy² + dz² - d(ct)²
with signature (+ + + -).
The two possibilities are perfectly equivalent, the chois between the one or another is purely a matter of convenience. In the first case the ds² is always positive inside the light cone. Some textbooks written by particles physicists do prefer the first choice. Of course all the interactions happens in the lightcone and the ds² is appreciately positive. At contrary, the relativists generally prefer the second choice, more elegant because it is a generalization of the ordinary metrics.
It should be noted that the quantity ds/c has a precise physical meaning: it's the proper time, experimented by the moving particle. Under that light, that means considered as a objective property, it is perfectly logical that ds is the same for every reference system.
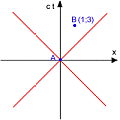
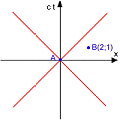
(4) - Let's consider two pairs of events. The first is causally connected, the second is not. Their coordinates are invented but in the first case B is in the lightcone of A, in the second case, is outside.
 |
 |
||
real time |
convention |
ds² = (ct)² - x² |
ds² = (ct)² - x² |
convention |
ds² = x² - (ct)² |
ds² = x² - (ct)² |
|
imaginary time |
convention |
ds² = (ct)² - x² |
ds² = (ct)² - x² |
convention |
ds² = x² - (ct)² |
ds² = x² - (ct)² |
As we can see, regardless the convention for ds², just the metric with the real time, with the signature (+ - - -) give a meaning to the casuality by distinguishing, through the sign, events causally connected from those not connected.
(5) - We can measure just the redshift and the apparent luminosity of distant supernovas. The former property is fundamental because the Hubble's law states a proportion between redshift and distance. Thus, by accurately measuring the redshift, we can derive the distance of the supernova. The problem that arise with distant supernovas is that we measure an apparent luminosity lower that expected for a supernova at a distance indicated according to the Hubble's law.
(6) - The digitized Frank Tipler's paper:
page 1 (GIF, 210 kb)
page 2 (GIF, 210 kb)
page 3 (GIF, 210 kb)
page 4 (GIF, 210 kb)
I want to thank John Baez, Alessandro Duci, Nicola Fusco, Valter Moretti and Piergiorgio Odifreddi for the interesting discussions; Mario Vitali and Pietro Rota to have sponsored the lessons.
To-do list:
- the concept of characteristic length in curved spaces
- the concept od geodetics
- the Lobacevskij experiment to measure the curvature of the Universe
- examples of curvature of tridimensional space
For feedback, comments or critics, please write to: sirtoli@uninetcom.it