RETE DI ERATOSTENE
Esperienze di astronomia con strumenti semplici








Il cerchio di Ipparco è uno dei più semplici strumenti solari. E’ costituito da un anello parallelo al piano dell’equatore celeste. La sua funzione è quella di individuare gli istanti degli equinozi. Durante gli equinozi, infatti, il Sole si trova
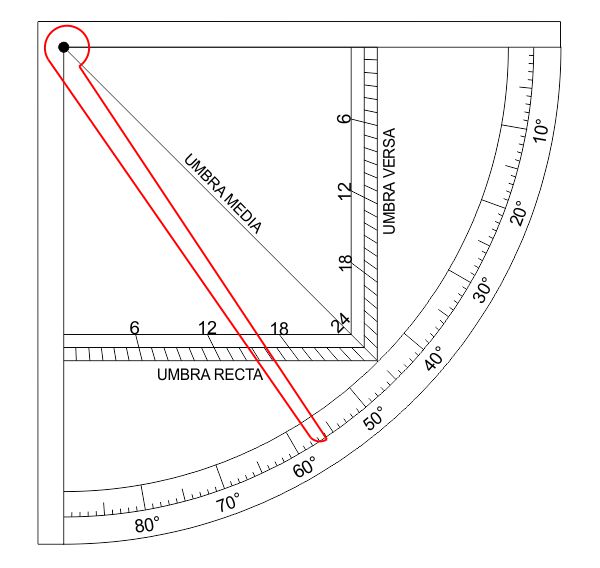
Il quadrato delle ombre è un antico calcolatore analogico di tangenti, strettamente legato all’uso dello gnomone. Esso simulava l’ombra di uno gnomone verticale (umbra recta) e, contemporaneamente quella di uno gnomone verticale (umbra versa). Il quadrante del 1568, firmato da
Raccolgo in queste pagine le descrizioni di alcuni semplici algoritmi riguardanti soprattutto le coordinate solari. Ho scelto gli algoritmi più semplici a discapito della precisione che in ogni caso è più che sufficiente nell’ambito degli scopi divulgativi del sito e
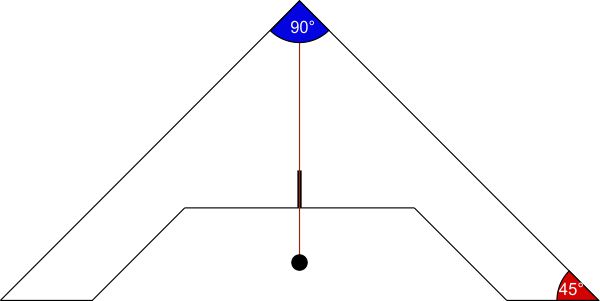
Archipenzolo in ottone del secolo XVII (Museo Galileo). Si potrebbe dire che l’archipendolo o archipezolo è l’antenato della livella. Permetteva non solo di controllare l’orizzontalità ma anche l’inclinazione di una superficie ed era usato nell’edilizia e in campo militare per
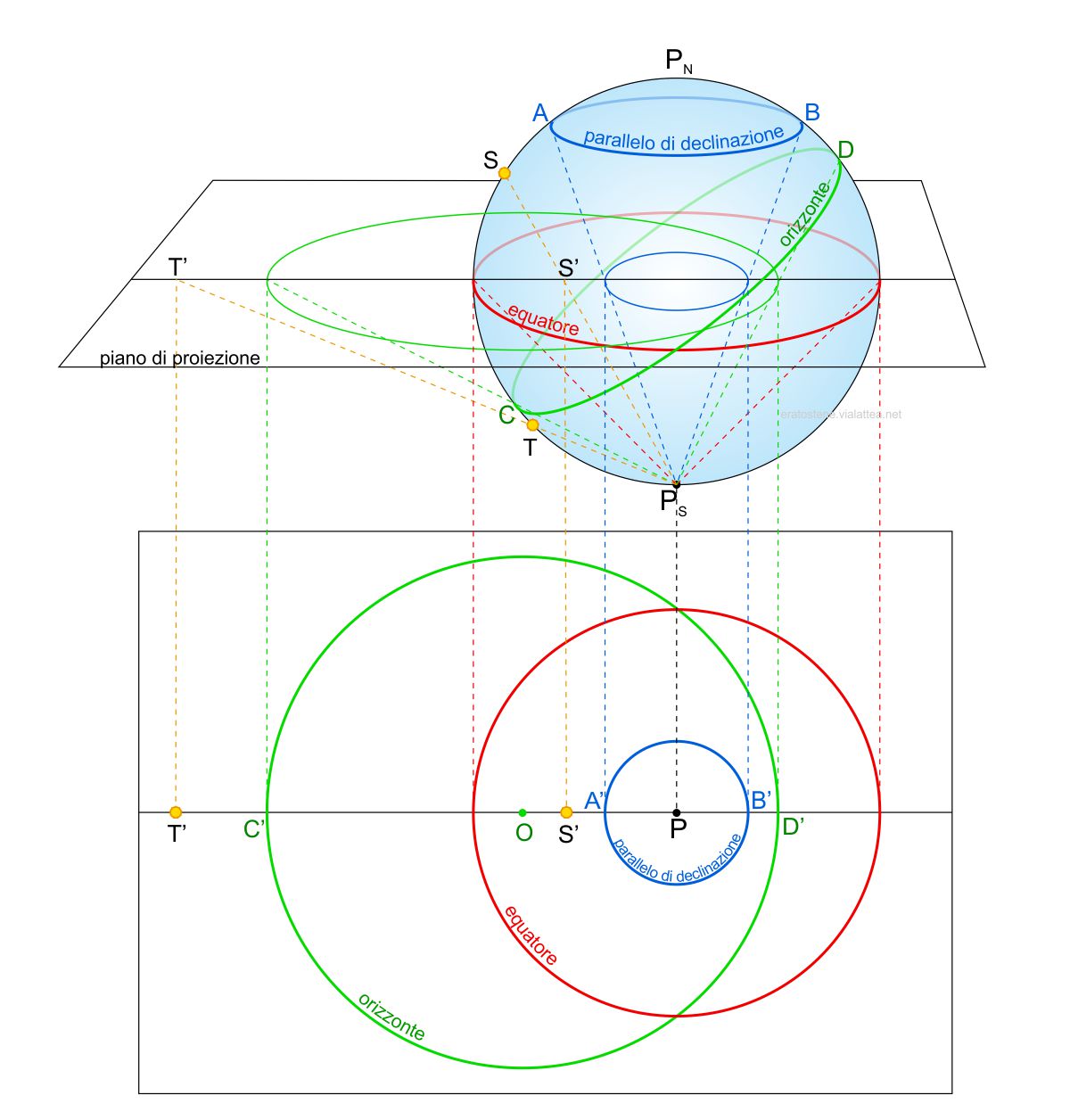
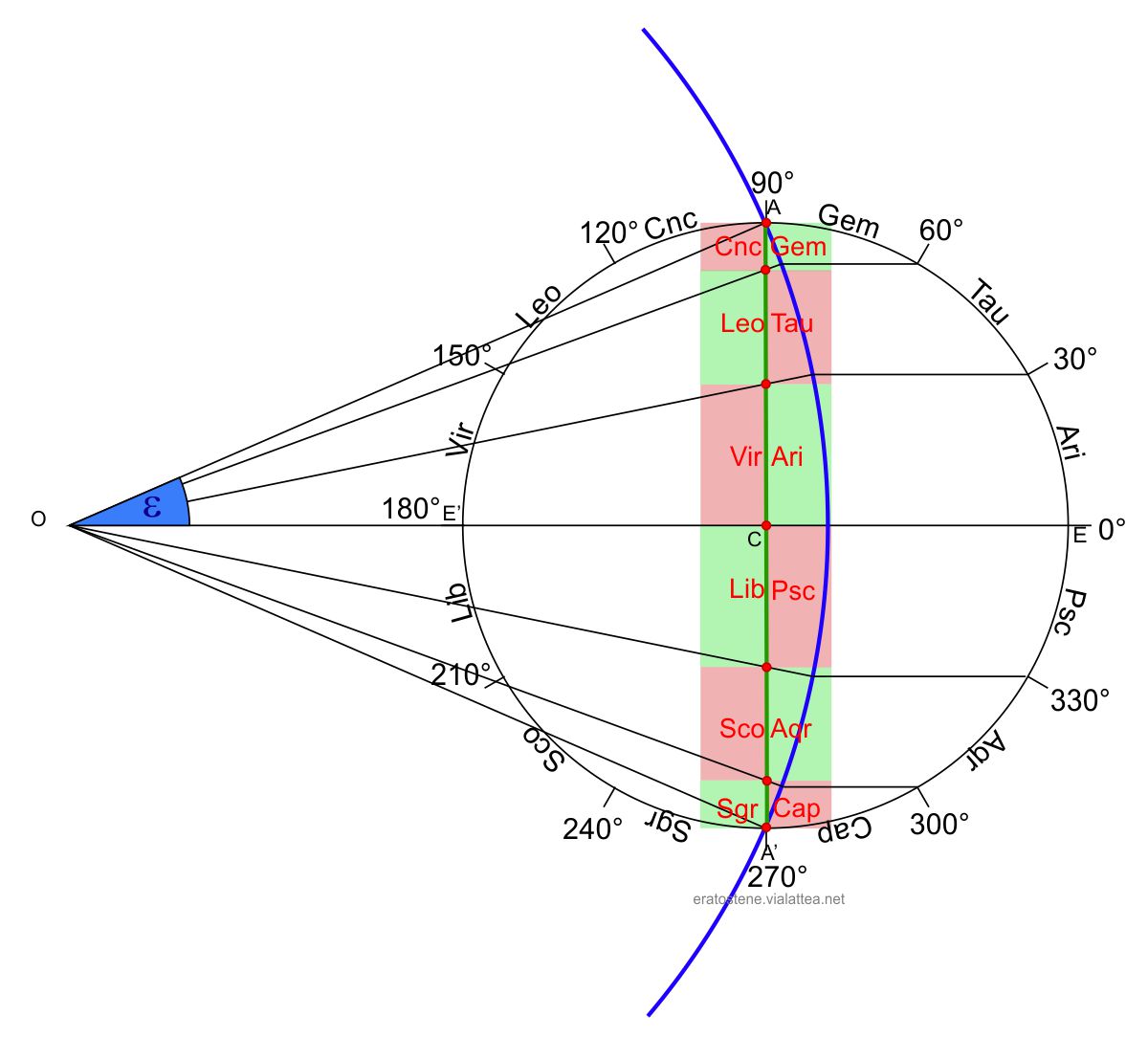
La proiezione stereografica è una funzione che proietta la superficie di una sfera su un piano in cui il punto di proiezione è un punto stesso della sfera. Tutti i punti della sfera hanno una loro immagine nel piano di
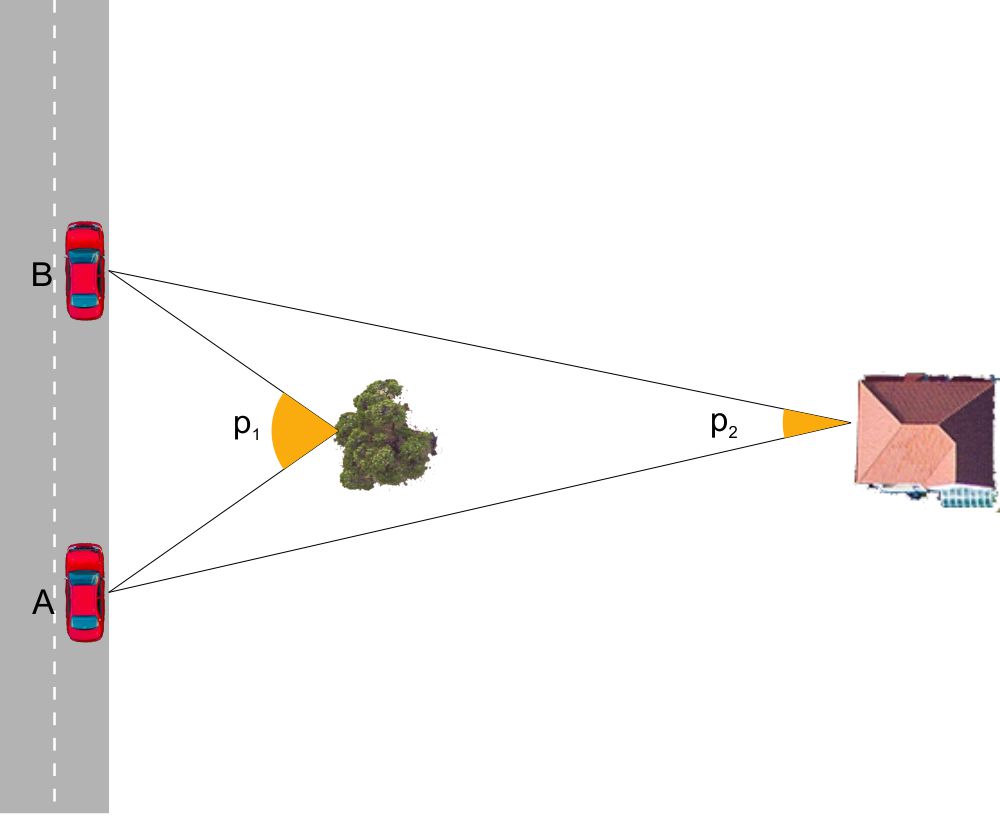
Durante un viaggio in automobile è esperienza comune quella di osservare dal finestrino in che modo gli elementi del paesaggio “si muovono” rispetto a noi e gli uni rispetto agli altri. Un albero che si trovano a poca distanza dalla
La linea meridiana segna la direzione nord-sud. Nel momento del passaggio del centro del disco solare al meridiano celeste superiore, l’ombra di uno gnomone verticale si trova nella direzione della linea meridiana. Con il seguente metodo (noto con il nome
Nell’Almagesto, Tolomeo (100-175 a.C.) descrive diversi strumenti per misurare la posizione del Sole. Il più interessante tra questi è il quadrante meridiano, noto come plinto di Tolomeo. E’ una lastra quadrata di pietra o di legno con un quadrante graduato
di Valerio Versari valerio.versari@virgilio.it Il globo celeste è il gemello del globo geografico, detto più comunemente mappamondo. Anziché rappresentare la Terra, esso rappresenta il cielo con le 88 costellazioni, l’equatore celeste, l’eclittica e la via lattea.
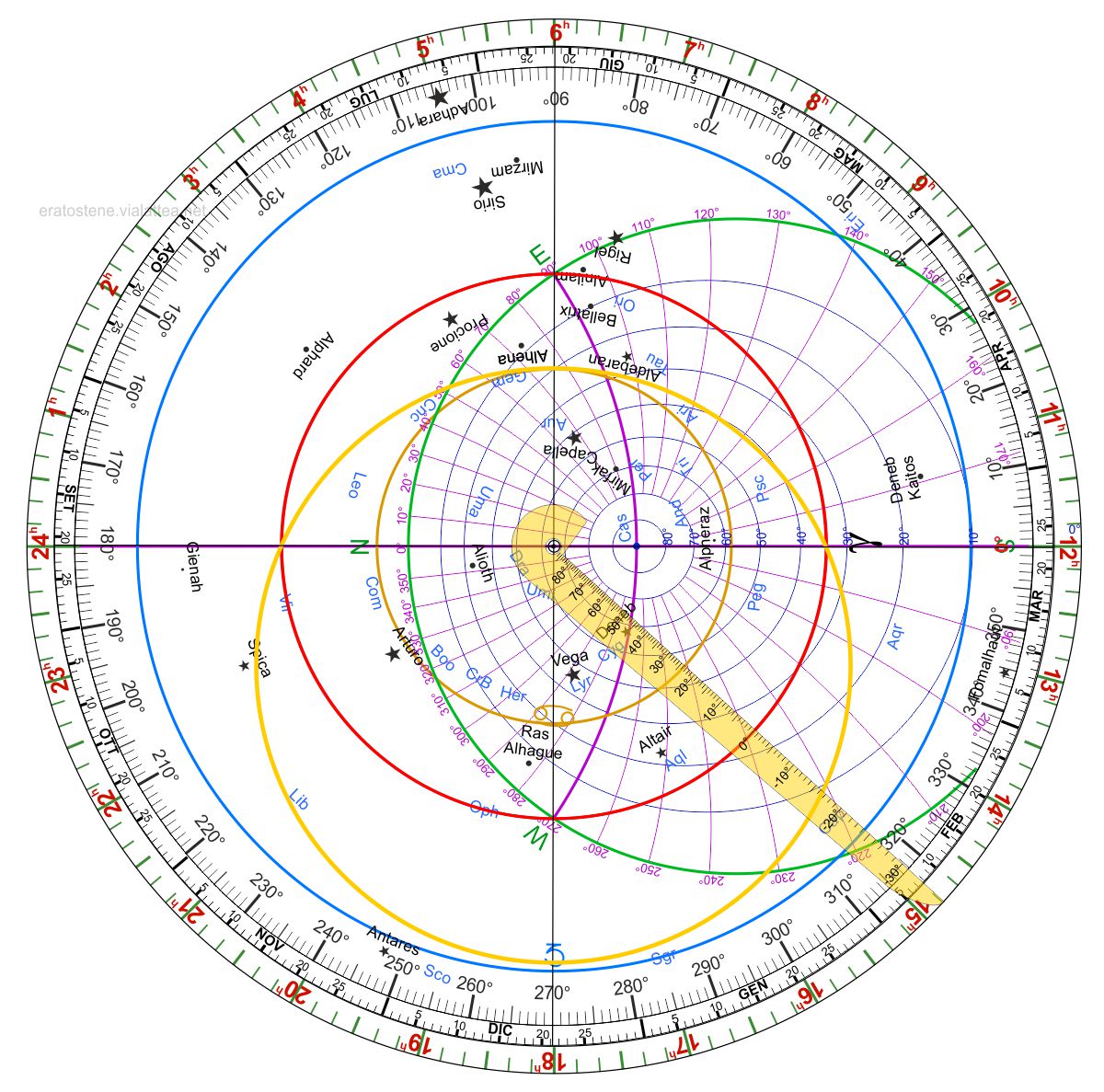
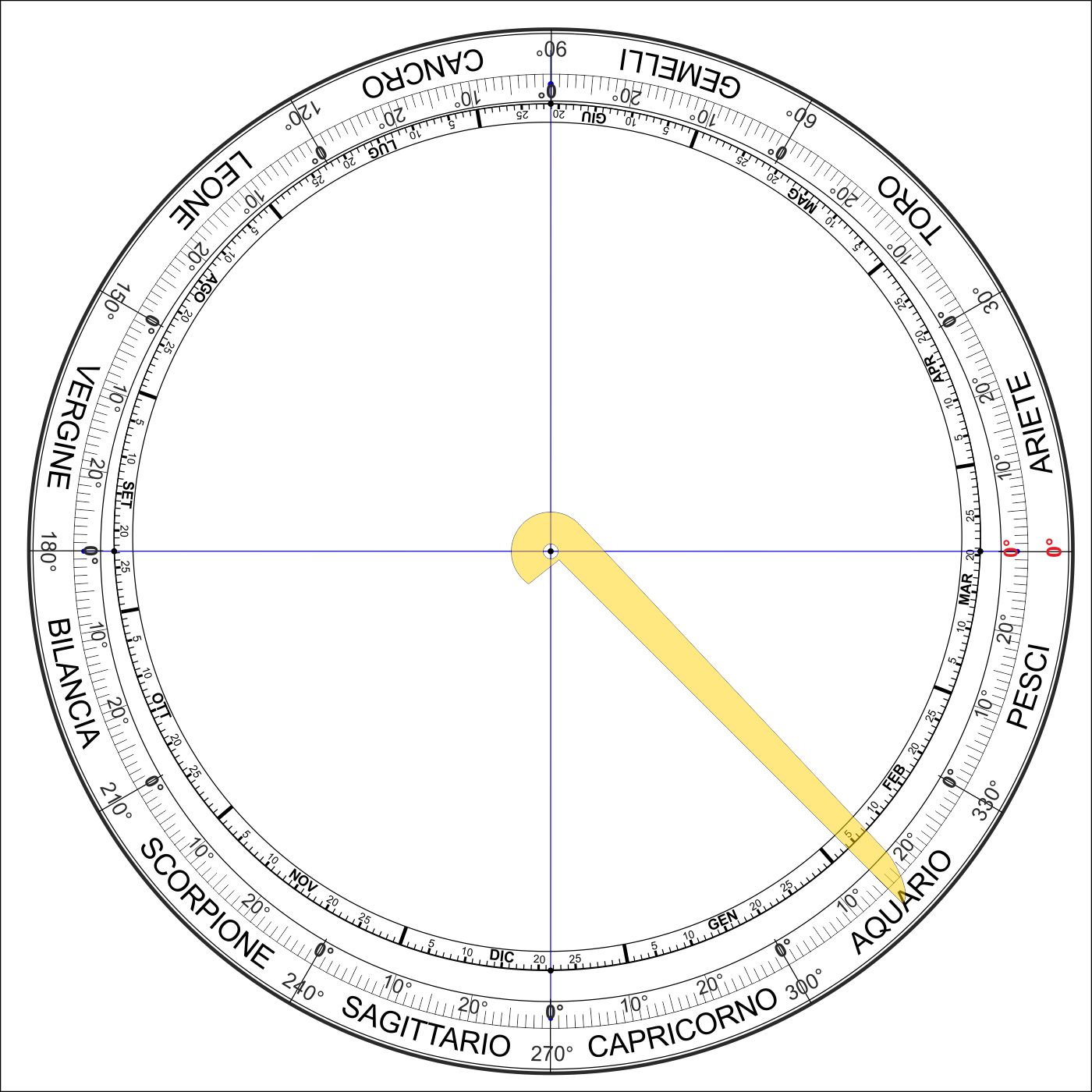
A nostro avviso, saper “leggere” le ore di notte con la semplice osservazione del cielo stellato, è un’esperienza stimolante e un’occasione per conoscere i principali movimenti della sfera celeste e del Sole. Orologio siderale di Theophili Bruni, 1640.Museo Storico Navale
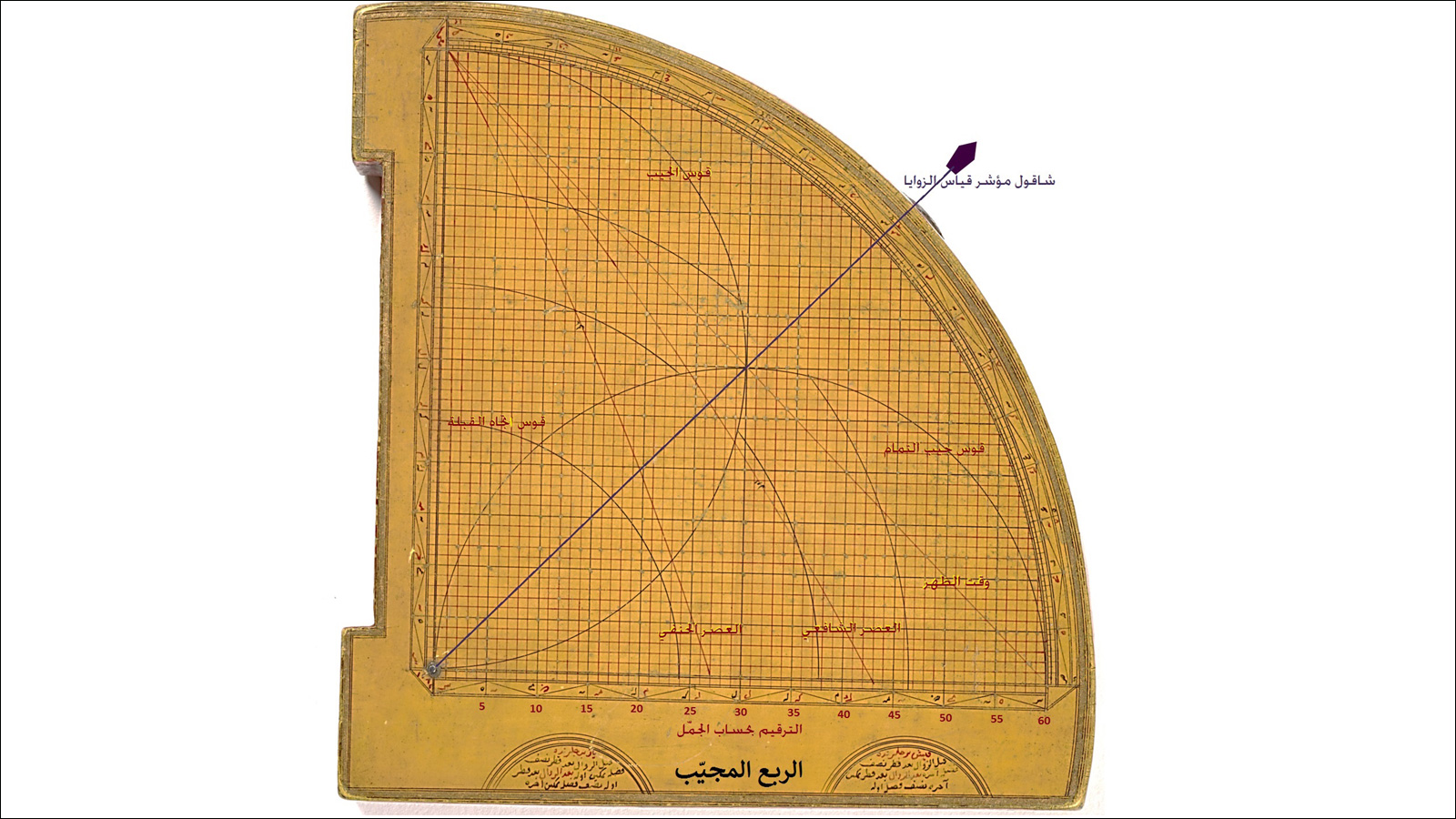
Il quadrante dei seni (الربع المجيب rubul mujayyab) era uno strumento computazionale ampiamente diffuso tra gli astronomi islamici a partire dal IX secolo fino al tardo XIX secolo. Descritto per la prima volta da Muhammad ibn Musa al-Khwarizmi, astronomo, matematico
Introduzione E’ una costruzione grafica descritta da Marco Vitruvio Pollione nel suo trattato De Architectura scritto intorno al 15 a.C. (vedi una traduzione in Liberliber.it). Il nono libro del trattato parla di astrologia, gnomonica, orologi solari, orologi ad acqua e,
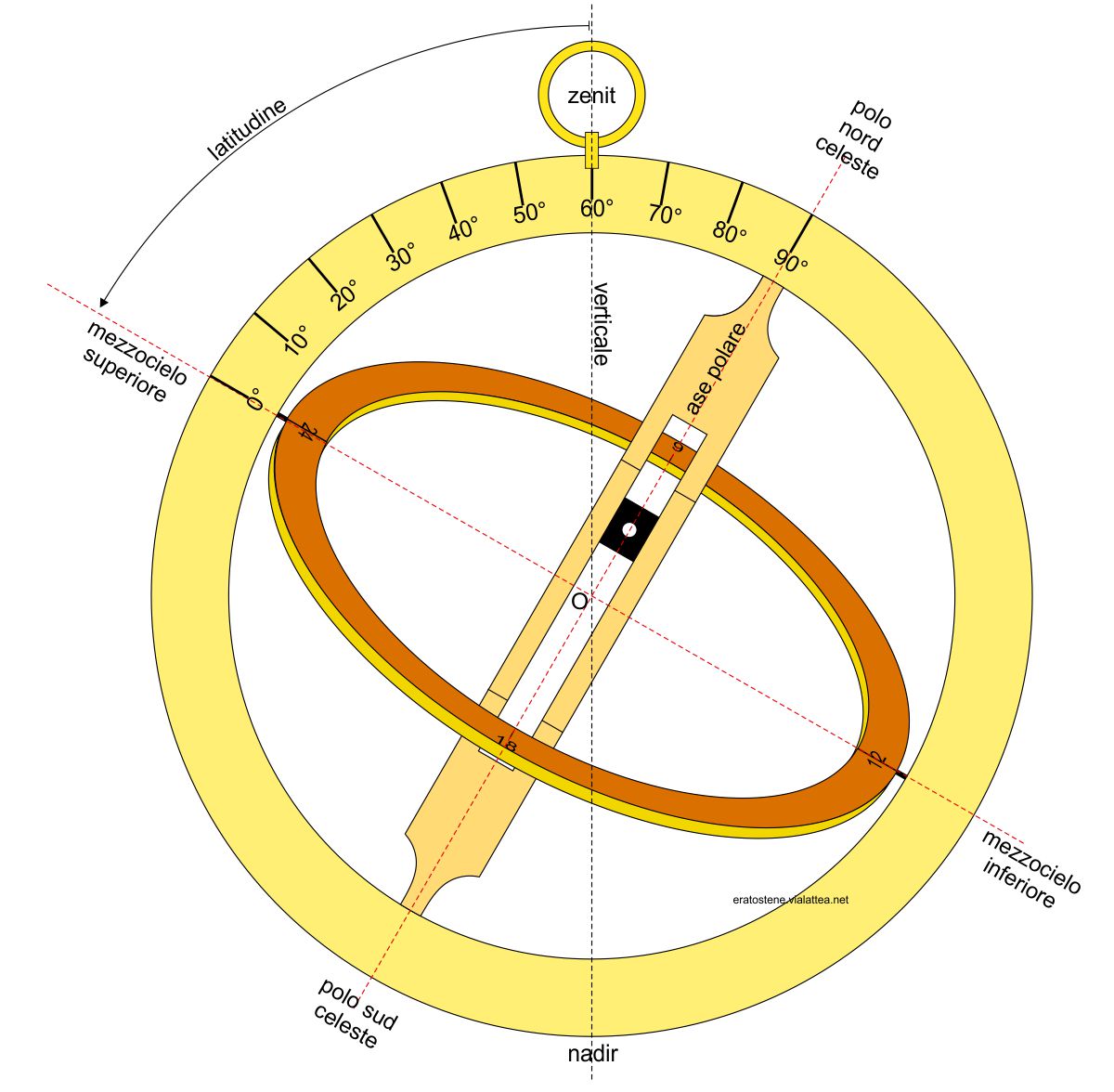
L’armilla o sfera armillare è un antico strumento astronomico usato sia per misurare le coordinate degli astri, sia come modello didattico della sfera celeste con i suoi principali circoli. I circoli erano rappresentati per mezzo di anelli(1) dotati di scale
E’ fra i più semplici orologi solari sia per la comprensione del loro funzionamento che per la costruzione geometrica. Lo strumento infatti non è altro che un modello della Terra orientata rispetto al Sole. Lo studio di un orologio equatoriale
Introduzione Descrizione generale Costruzione di un astrolabio semplificato Le basi della lamina: equatore e orizzonte Disegnare i tropici Gli almucantarat o cerchi di altezza I cerchi verticali La scala stereografica della declinazione La scala delle ore La rete: disegnare l’eclittica
L’equatorium solare era uno strumento che serviva per ottenere la longitudine eclittica del Sole in qualsiasi giorno dell’anno. Questo nome deriva dal termine equazione che aveva un significato diverso da quello matematico attuale. Con equazione si intendeva la differenza tra
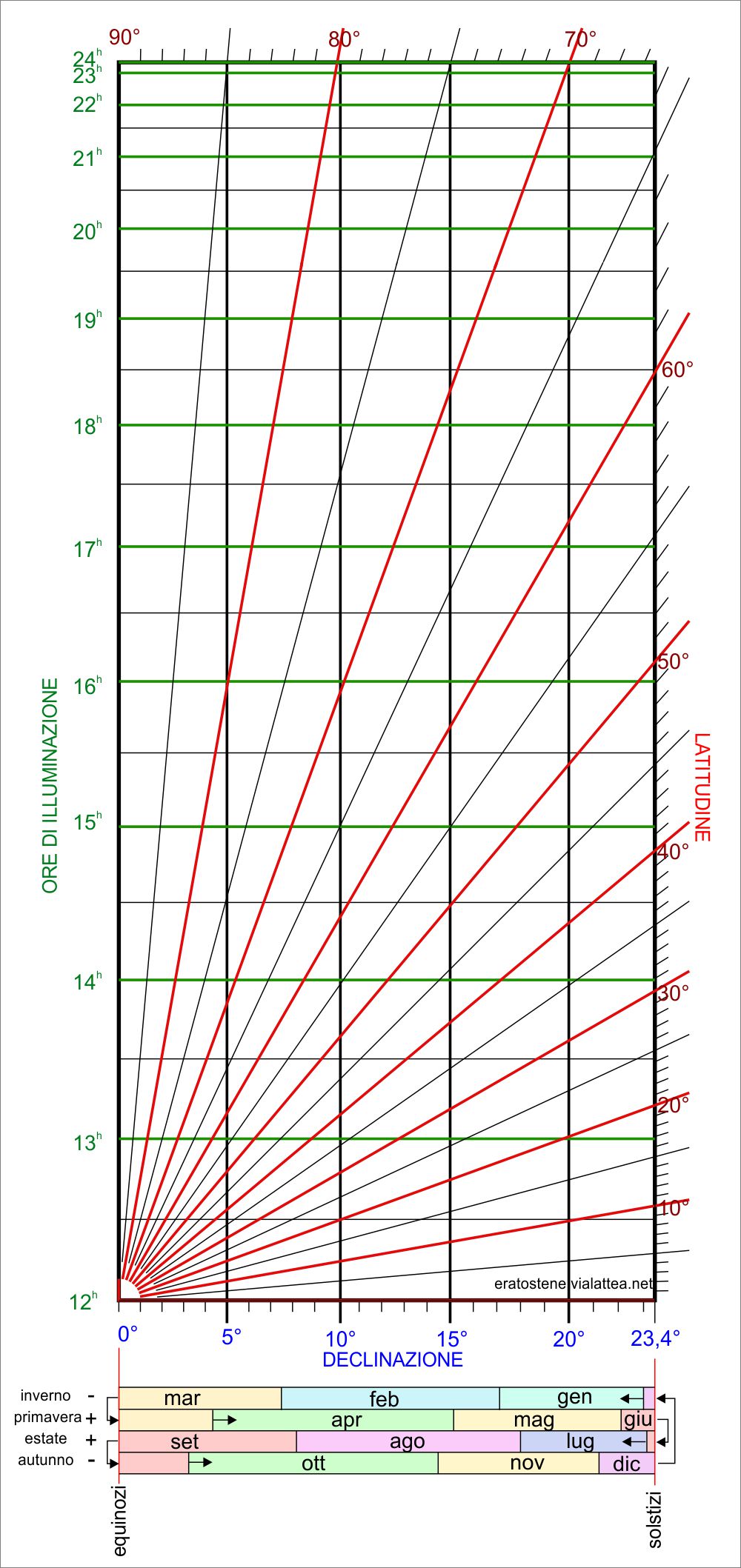
Il punto del sorgere e il punto del tramonto del Sole sono legati alla sua declinazione e alla latitudine del luogo. Da questi due importanti parametri dipendono anche la lunghezza dell’arco diurno del Sole. Se la lunghezza dell’arco diurno varia,
Tra gli orologi solari, l’anello equinoziale è uno degli strumenti più interessanti sia per la semplicità di progettazione che per l’adattabilità di utilizzo. Descriviamo innanzitutto uno dei bellissimi strumenti presenti nella collezione del Museo di Storia della Scienza di Oxford,
I costruttori di orologi solari si trovavano spesso di fronte al problema di mettere in relazione le date del calendario con la declinazione del Sole. Un esempio è descritto in queste pagine nella costruzione dell’anello equinoziale e un altro esempio