Nel XIX secolo Gauss, studiando la teoria degli errori, si
imbattè nella seguente funzione:
 con
con

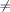 0 e
0 e 
costanti reali arbitrarie,
oggi di fondamentale importanza in statistica e in calcolo
delle probabilità, nota come funzione gaussiana o funzione
normale o, per la sua particolare forma del grafico (figura 1), curva
a campana e le cui salienti caratteristiche sono elencate di seguito:
-
è definita in tutto l’asse reale;
-
è sempre positiva;
-
è crescente per x <
 , decrescente per x >
, decrescente per x >  e
e
assume un massimo per x = ;
; -
tende a 0 sia per x che tende a –
 che per x che tende a +
che per x che tende a + ;
; -
è dotata di derivate di ordine comunque elevato,
ossia, come dicono i matematici, è “di classe C-infinito”. -
il grafico della funzione è simmetrico rispetto
alla retta x = ;
; -
possiede due flessi rispettivamente nei punti
 –
–  e
e  +
+  .
.

Figura 1. Grafico
di N(x).
Dopo questa breve presentazione della funzione gaussiana,
adesso veniamo al nocciolo della domanda. Nella teoria delle funzioni a
variabile reale sussiste un importante teorema di esistenza delle funzioni
primitive, secondo il quale ogni funzione f(x) continua in un
intervallo I, ammette primitiva in I, ossia una funzione
F(x), tale che
D F(x) = f(x). Poiché
N(x) è continua su tutto l’asse reale, ammette
sicuramente una primitiva su tutto l’asse reale. Come moltissimi teoremi di
esistenza che si trovano in matematica, anche questo ha un grave difetto, non
indica in che modo la primitiva può essere calcolata, quindi ci
troviamo di fronte alla seguente situazione: sappiamo che esiste una funzione
G(x), primitiva di N(x), ma non siamo in grado di
calcolarla. In realtà ciò non è del tutto esatto,
perchè il modo di calcolare la primitiva in questo teorema di
esistenza viene fornito ma la strada che indica non è molto
praticabile, infatti considerata una funzione f(x) continua in
[a, b], la funzione F(x) :=  è una sua primitiva in
è una sua primitiva in
[a, b]. Questo è un integrale definito che si
calcola usando il famoso teorema di Torricelli, altrimenti detto teorema
fondamentale del calcolo integrale: considerata una funzione
f(x) continua in [a, b], se
F(x) è una sua primitiva, allora  . Come è noto,
. Come è noto, 
rappresenta l’area sottesa dalla funzione f(x) nell’intervallo
[a, b]. Per calcolare la primitiva occorre saper
calcolare l’integrale definito e per calcolare quest’ultimo occorre saper
calcolare la primitiva, accade un po’ come il gatto che si morde la coda. In
effetti però la primitiva di una funzione si calcola con altri metodi,
ad esempio procedendo con l’integrazione per parti. Comunque eccettuati rari
e semplici casi, non siamo mai in grado di calcolare la primitiva di una data
funzione f(x), a differenza di come avviene per la derivata;
data una funzione siamo quasi sempre in grado di trovare la sua derivata,
usando le varie regole di derivazione.
Quadratura numerica
Nei casi in cui non
siamo in grado di calcolare analiticamente la primitiva della funzione
f(x), si deve ricorrere al calcolo dell’integrale con tecniche
di approssimazione numerica le quali essenzialmente consistono
nell’approssimare, nell’intervallo [a, b], la funzione
f(x) con un’opportuna famiglia di funzioni
{gn(x) | n 
 } facilmente integrabili analiticamente
} facilmente integrabili analiticamente
in [a, b] e che al crescere di n si “avvicinano”
sempre di più a f(x), ossia, detto in modo un po’
più formale, comunque scegliamo un numero  > 0, esiste un numero naturale n, per
> 0, esiste un numero naturale n, per
il quale accade che
|f(x) – gn(x)| <  per ogni x
per ogni x  [a, b], come illustrato nella figura 2.
[a, b], come illustrato nella figura 2.

Figura 2.
Approssimazione uniforme.
Un esempio di questa categoria di funzioni può essere
fornita da una opportuna famiglia di polinomi approssimanti
f(x), come per esempio i polinomi interpolanti di Lagrange.
Procedendo in questa maniera si vanno a calcolare gli integrali  . A seconda delle proprietà di
. A seconda delle proprietà di
f(x) e di come si sceglie la successione
(gn(x))n, la successione ( )n può convergere,
)n può convergere,
oppure no, al valore  e se converge lo
e se converge lo
può fare più o meno lentamente.
Tra le innumerevoli funzioni
di cui non siamo in grado di trovare la primitiva in modo analitico vi è
anche la funzione N(x); per l’importanza fondamentale
che riveste in statistica e nel calcolo delle probabilità, una sua primitiva,
che viene indicata con erf(x), è stata calcolata numericamente
per molti valori della variabile x e tabulata. Con l’avvento dei
personal computer molti software matematici calcolano erf(x) con metodi
di approssimazione numerica.
Più
precisamente, erf(x) è la primitiva di N(x) nel
caso in cui sia  = 1 e
= 1 e  = 0,
= 0,
ossia nel caso si tratti della cosiddetta funzione normale standard. Da
questa primitiva, mediante facili trasformazioni, si può risalire alle
primitive di tutte le altre funzioni N(x).
Metodo di Bézout
Considerata una funzione
f(x) continua nell’intervallo [a, b], scelti
n + 1 punti equispaziati,
a = x0, x1, …, xn = b,
detti nodi e ponendo
yi = f(xi), l’idea
è quella di sostituire alla funzione f(x) all’interno di
ogni intervallino [xi-1, xi]
un polinomio di primo grado, ossia una retta o, per meglio dire, con un
segmento avente per estremi i punti di coordinate
(xi-1, yi-1) e
(xi, yi), formando così una
strana figura che prende il nome di trapezoide, la cui forma è
mostrata in figura 3; l’unione di questi n segmenti rappresenta la
funzione approssimante gn(x).

Figura 3.
Approssimazione alla Bézout.
Come si vede dalla figura, si vengono a formare n
trapezi e l’area del generico trapezio i-esimo è
(xi – xi-1)(yi + yi-1) / 2,
quindi l’area del trapezoide è

tenendo presente che
(xi – xi-1) = (b – a) / n.
Indicando con En l’errore che si commette approssimando
 con Sn allora si ha che
con Sn allora si ha che
 = Sn + En
= Sn + En
e, se En tende a 0 al crescere di n, accade che
Sn tende a  . In
. In
particolare, se f è dotata di derivata seconda continua allora
si dimostra che
En = f”(c) (b – a) / 12n2,
dove c è un punto interno all’intervallo
[a, b] a noi non noto (se fosse noto sapremmo il valore
esatto dell’integrale) e indicando con K1 la
quantità
K1 := f”(c) (b – a) / 12,
costante rispetto a n, abbiamo che
En = K1 / n2.
In questo caso quindi En si avvicina a 0 all’aumentare del
numero del numero dei nodi, e pertanto Sn si avvicina a
 .
.
Ovviamente noi possiamo
calcolare solo un numero finito di questi Sn, bisogna
trovare un criterio per fermarci a un opportuno indice. Un sistema per fare
ciò è quello di fissare a priori un numero opportunamente
piccolo  > 0 e calcolare le differenze
> 0 e calcolare le differenze
|S1 – S0|,
|S2 – S1|, …,
|Sk – Sk-1|, … fino a
quando non si giunge a un indice n per il quale risulti
|Sn – Sn-1| <  ; Sn è il valore che viene scelto
; Sn è il valore che viene scelto
per approssimare l’integrale.
Metodo di Cavalieri-Simpson
Si considerano
2n + 1 punti equispaziati,
a = x0, x1, …,
x2n = b di modo che
[a, b] risulti suddiviso in n intervalli del tipo
[x2k, x2k+2] con
k = 0, 1, …, n ossia
[a, b] = [x0, x2] U [x2, x4] U … U [x2n-2, x2n]
e in ognuno di questi si sostituisce la funzione f(x) con un
polinomio di secondo grado, ossia con una parabola, che indichiamo con
Pk, avente l’asse parallelo all’asse y e passante
per i punti del piano di coordinate
(x2k, y2k),
(x2k+1, y2k+1),
(x2k+2, y2k+2) e in
questo caso la funzione approssimante gn(x) è
l’unione di tutti questi polinomi Pk. Si calcola l’area
S’n, somma di tutte le aree sottese dalle parabole
Pk nell’intervallo
[x2k, x2k+2]. Ciascuna
di queste aree vale
(y2k + 4y2k+1 + y2k+2)(b – a) / 6
e quindi  , per cui
, per cui  = S’n + E’n
= S’n + E’n
dove E’n è l’errore e se esso tende a 0 allora
S’n tende a  .
.
Se f è
dotata di derivata seconda quarta, l’errore che si commette è
E’n = f(4)(c) (b – a)5 / 2880n4,
dove c è un punto interno all’intervallo
[a, b] a noi non noto, e indicando con
K2 la quantità
K2 := f(4)(c) (b – a)5 / 2880,
costante rispetto a n, si ha allora che
E’n = K2 / n4.
In questo caso quindi E’n si avvicina a 0 all’aumentare del
numero del numero dei nodi, e pertanto S’n si avvicina a
 .
.
Abbiamo visto che, in
opportune ipotesi sulla funzione f(x), i due procedimenti sono
entrambi convergenti, ma confrontando i due errori:

si nota che E’n tende molto più
velocemente a zero rispetto a En al crescere di n;
quindi se f(x) è una funzione dotata di derivata quarta
continua è conveniente usare il procedimento di Cavalieri-Simpson
perchè si raggiunge il risultato voluto in un numero minore di passi
facendoci risparmiare tempo.
Come nel caso delle
formule di Bézout, si considera la successione S’1,
S’2, …, S’n, …: se essa converge
allora si fissa un  > 0 molto piccolo, si
> 0 molto piccolo, si
calcolano le differenze
|S’1 – S’0|,
|S’2 – S’1|, …,
|S’k – S’k-1|, … e si
considera come risultato approssimato di 
la quantità S’n per la quale risulta
|S’n – S’n-1| <  .
.
Finora ci siamo occupati degli integrali propri,
ossia integrali i cui estremi a e b siano finiti. Che cosa
succede se uno degli estremi è infinito, ossia se si vuole calcolare
 , dove ad esempio f(x)
, dove ad esempio f(x)
può essere la funzione gaussiana?
Le formule usate fino a
questo momento non vanno più bene, ma si devono considerare formule
alquanto complicate che non è il caso neanche da accennare. Comunque
la cosa importante da sottolineare è che in questo caso si sostituisce
f(x) con una successione di funzioni più facilmente
integrabili.
Impaginato da Gino Favero