La domanda posta richiede una risposta più lunga,
approfondita e elaborata di quanto è opportuno trattare in questo
spazio, quindi in questa pagina riporto solo i fatti salienti e passaggi
più delicati mettendo in evidenza gli aspetti generali dell’argomento
evitando i noiosi calcoli, per i quali rimando ai siti elencati alla fine di
questa breve esposizione.
Nozioni generali sulle equazioni algebriche
Considerato un polinomio
Pn(x) = anxn + an-1xn-1 + … + a1x + a0
di grado n, è detto zero di
Pn(x) un qualsiasi numero z (reale o
complesso) per il quale si abbia
Pn(z) = anzn + an-1zn-1 + … + a1z + a0 = 0.
Risulta subito evidente che, in base alla definizione appena enunciata, la
ricerca degli zeri di Pn(x) è equivalente
alla ricerca delle soluzioni (radici) dell’equazione algebrica:
anxn + an-1xn-1 + … + a1x + a0 = 0.
(1)
Si può facilmente dimostrare che se z è
uno zero di Pn(x) allora il polinomio
x – z divide Pn(x) e
viceversa, se x – z divide
Pn(x), allora z è uno zero di
Pn(x). Se indichiamo con
Pn-1(x) il polinomio quoziente di questa
divisione, può capitare che z sia anche uno zero di questo
polinomio e in tal caso si dimostra che il polinomio
(x – z)2 divide
Pn(x): in tal caso, z è detto zero
di molteplicità 2. In generale, se
(x – z)k divide
Pn(x), allora z è detto zero di
molteplicità k e, in analogia a tale terminologia, z,
è detta soluzione k-upla dell’equazione (1). Il teorema
fondamentale dell’algebra afferma che Pn(x)
ammette esattamente n zeri, a patto di considerare ciascuno di essi
con la propria molteplicità, ossia, se z1,
z2, …, zm sono zeri di
molteplicità rispettivamente k1,
k2, …, km, allora
k1 + k2 + … + km = n
e Pn(x) si può scrivere nel seguente modo:
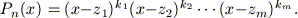
Un altro risultato importante è che se
z = a + ib è una radice
complessa di Pn(x), allora anche il suo complesso
coniugato z’ = a – ib è una
radice di Pn(x); da questo segue immediatamente che
se n è dispari l’equazione (1) ammette almeno una soluzione
reale, mentre se n è pari essa potrebbe ammettere solo
soluzioni complesse non reali.
Equazione di terzo grado
Considerata l’equazione
di terzo grado
ax3 + bx2 + cx + d = 0
(2),
per quanto prima asserito si possono verificare i seguenti
casi:
-
3 soluzioni reali distinte z1,
z2, z3; -
3 soluzioni reali coincidenti, ossia un’unica soluzione
z di molteplicità 3 (radice tripla); -
3 soluzioni reali di cui due coincidenti, ossia una
radice doppia z1 e una radice semplice
z2; -
1 soluzione reale z1 e due soluzioni
complesse coniugate z2, z’2.
Operando la sostituzione
y = x + b / 3a,
l’equazione (2) diviene:
y3 + 3py – 2q = 0
con 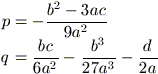 ,
,
(3)
alla quale si dà il nome di equazione
depressa. Operando la sostituzione
y = (z – t) essa diventa
(z – t)3 + 3p(z – t) – 2q = 0.
(4)
Tenendo presente che comunque si scelgano due numeri
complessi z e t, è sempre verificata l’identità
(z – t)3 + 3zt(z – t) – (z3 – t3) = 0,
e confrontando quest’ultima con la (4), abbiamo che z e t
devono soddisfare il seguente sistema:
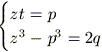
(5)
Dalla prima della (5) si ricava
t = p / z e dalla seconda
z3 – (p / z)3 = 2q
da cui
z6 – 2qz3 – p3 = 0,
che con la sostituzione u = z3 diventa
un’equazione di secondo grado nell’incognita u,
u2 – 2qu – p3 = 0.
Risparmiandoci inutili e tediosi calcoli diciamo solamente che una volta
trovate le due soluzioni u1 e u2 si
calcolano 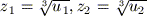 e
e
t1 = p / z1,
t2 = p / z2 da cui si
ricava
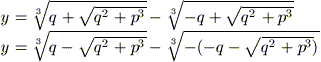
Osserviamo che queste due soluzioni coincidono (attenzione:
sono la stessa soluzione, non si tratta una radice di molteplicità 2).
Infatti,
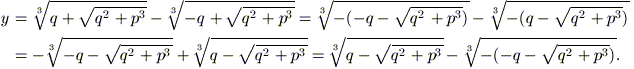
Come però detto in precedenza, un’equazione di terzo
grado ammette 3 soluzioni, quindi dobbiamo cercare le altre due. Per fare
ciò indichiamo con s l’unica soluzione fino a questo momento
trovata, 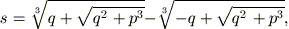 ; poniamo
; poniamo 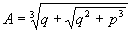 e
e 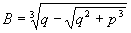 e dividiamo l’equazione
e dividiamo l’equazione
(3) per il polinomio (y – s), ottenendo in questo
modo l’identità
y2 + sy + (s2 + 3p) = 0,
la quale è un’equazione di secondo grado. Risolvendo quest’equazione
e tenendo presente che, come si può dimostrare (vi risparmio i
calcoli), 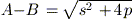 si ottengono le tre soluzioni
si ottengono le tre soluzioni
cercate dell’equazione (3):
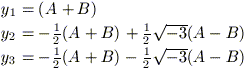
Infine, ricordando che
y = x + b / 3a, si
ottengono le soluzioni dell’equazione (2):
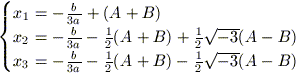
con 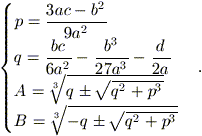
Il fatto che nella seconda e nella terza soluzione compaia
un numero immaginario (la radice quadrata di -3) non implica necessariamente
che le due radici siano complesse, così come la prima radice
può essere complessa anche se dalla sua espressione questo termine non
appaia esplicitamente. Tutto dipende dai valori che assumono p e
q, quindi A e B. Un ruolo importante lo svolge il
discriminante 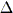
= q2 + p3 e in
particolare:
-
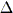 > 0,
> 0,
allora A e B sono reali; tali sono anche la loro somma e la
loro differenza. Ne segue che in questo caso l’equazione ha una radice reale
e due radici complesse coniugate. -
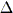 = 0,
= 0,
allora A e B sono reali ed uguali; l’equazione ha tre radici
reali delle quali due coincidenti (la seconda e la terza delle formule). Se
poi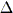 = 0 perché
= 0 perché
p = q = 0, le tre le radici sono
coincidenti nel valore x = –b / 3a. -
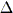 < 0,
< 0,
allora le tre radici sono reali e distinte.
L’aspetto più strano in quest’ultimo caso è
che, per trovare i valori reali delle tre radici, occorre trattare i numeri
complessi che compaiono sotto il segno delle radici cubiche.
Equazione di quarto grado
Passiamo adesso alla
risoluzione delle equazioni di quarto grado
ax4 + bx3 + cx2 + dx + e = 0
(8)
(ipotizziamo che sia a > 0, posizione che
non lede la generalità del procedimento). Con il cambio di variabile
x = y – b / 4a, si
ottiene
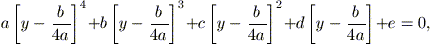
la quale, dopo vari calcoli diviene:
y4 + 2Ay2 – By – C = 0
con 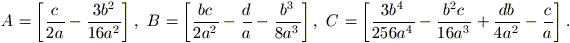
Aggiungendo
A2 ad entrambi i membri si ha
y4 + 2Ay2 + A2 = A2 + By + C;
tenendo presente che al primo membro si ha un quadrato
perfetto, abbiamo
(y2 + A)2 = A2 + By + C.
Aggiungendo poi
w2 + 2Aw + 2wy2,
con w da determinare in modo che al secondo membro si abbia un
quadrato, otteniamo
(y2 + A + w)2 = 2wy2 + By + (w2 + 2Aw + A2 + C).
Affinché al secondo membro ci sia un quadrato
perfetto deve risultare che il suo discriminante (rispetto a y) sia
uguale a 0, ossia 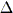 = B2 – 8w(w2 + 2Aw + A2 + C) = 0
= B2 – 8w(w2 + 2Aw + A2 + C) = 0
da cui
8w3 + 16Aw2 + 8(A2 + C)w – B2 = 0
la quale è un’equazione di terzo grado, ed ammette
almeno una soluzione reale che indichiamo con W, per cui si ha
(y2 + A + W)2 = 2W(y + B / 4W)2
e, ponendo H = (2W)1/2,
(y2 + A + W)2 = H2(y + B / 4W)2,
che fornisce due equazioni di secondo grado:
y2 + Hy + (A + W – HB / 4W) = 0,
y2 – Hy + (A + W + HB / 4W) = 0,
le quali, risolte, danno le soluzioni cercate.
Equazioni di grado superiore al quarto.
L’equazione algebrica
(1) si dice risolubile per radicali se le sue soluzioni sono
ottenibili con un numero finito di operazioni razionali (addizioni,
sottrazioni, moltiplicazioni, divisioni) ed estrazioni di radice. Le
equazioni di secondo, terzo e quarto grado sono risolubili per radicali. Nel
tentativo di trovare le soluzioni delle equazioni di grado superiori al
quarto i matematici hanno scoperto le seguenti relazioni tra i coefficienti
dell’equazione (1) e le sue radici z1,
z2, …, zn:
Queste relazioni, dovute a Viete, risultano fondamentali
nella dimostrazione (che qui omettiamo per la sua complessità, in
quanto fa uso dei concetti di strutture algebriche quali i campi, gruppi di
simmetria e gruppi ciclici) del
Teorema (di Abel-Ruffini): in generale,
un’equazione di grado superiore al quarto (n  5) non è risolubile per radicali.
5) non è risolubile per radicali.
Questo teorema non afferma che qualunque equazione di
grado n  5 non è
5 non è
risolubile per radicali, ma che esistono equazioni non risolubili per
radicali. Per esempio,
x5 + x + 1 = 0 non
è risolubile per radicali, mentre
x5 – x4 – x + 1 = 0
lo è.
Bibliografia e approfondimenti
http://www.matematicamente.it/approfondimenti/Equcub.doc
http://web.unife.it/altro/tesi/A.Montanari/algebra.htm
http://www.mbservice.it/scuola/tartaglia/le_equazioni_di_terzo_grado.htm
http://www.dimi.uniud.it/~gorni/Dispense/TerzoGrado.pdf