È vero, il problema sottoposto dal lettore è
decisamente complicato. Niente male come esordio, no? Mi si lasci anche
aggiungere che la suddivisione in “sottoproblemi” proposta dal lettore non ci
sarebbe di nessun aiuto, perchè il fatto di sapere quale carta viene
messa in tavola dal giocatore “primo di mano” non ci è di nessun
aiuto: per fare “scopa” la condizione è quella di avere in mano una
carta dello stesso valore, non importa quale esso sia (preciso che mi
riferisco al gioco dello scopone scientifico, senza “scopa d’asso”). È
invece decisamente buona (come sempre!) l’idea di scomporre il problema in
altri problemi più piccoli e semplici, sperando che unirne le
soluzioni dia in modo altrettanto semplice la soluzione del problema di
partenza.
La chiave per scomporre
il problema, come spesso accade con i problemi di probabilità,
è la cosiddetta formula delle probabilità totali: se
A1, A2, …, An
è una famiglia di eventi (cioè di insiemi di “casi”, laddove
“caso” è un termine leggermente improprio rispetto all’ufficiale
“evento elementare” ma — credo — comprensibile in modo piuttosto diretto)
la cui unione esaurisce tutti i casi possibili, allora per ogni evento
B vale la relazione
P(B) = P(B|A1)P(A1) + P(B|A2)P(A2) + … + P(B|An)P(An),
dove con la scrittura P(B|A) si indica
la probabilità condizionata dell’evento B rispetto
all’evento A, che si calcola secondo la formula
P(B|A) = P(B 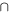 A) / P(A) (per qualche
A) / P(A) (per qualche
dettaglio in più sulla probabilità condizionata e sul modo in
cui può essere calcolata negli spazi di probabilità uniforme si
dia un’occhiata anche alla mia risposta
sul lancio ripetuto di una moneta). Notiamo che perché la nozione di
probabilità condizionata abbia un significato, bisogna supporre che
l’evento condizionante sia maggiore di zero: tale ipotesi si deve allora
applicare a tutti gli eventi condizionanti A1,
A2, …, An nella formula delle
probabilità totali.
Tentiamo di applicare
questa formula al caso del gioco dello scopone. Per comodità di
riferimento, mi si permetta di chiamare (prendendo a prestito una
consuetudine che si usa nel gioco del bridge) S (“sud”) il primo
giocatore di mano e E (“est”) il secondo. Chiamiamo B l’evento
“E possiede la carta che ha giocato S” (cioè, E
è nelle condizioni di poter fare scopa e si suppone quindi che la
faccia) e calcoliamo le probabilità condizionate ai quattro eventi
Ai = “S ha giocato una carta di un gruppo
di i“, con i che varia da uno a quattro. Per esempio, insomma,
l’evento A2 indica il fatto che S aveva in mano una
coppia di carte di un certo valore (non importa quale) e ha scelto di giocare
una di quelle due, così come l’evento A4 indica il
fatto che S aveva in mano tutte e quattro le carte di un certo valore
e ne ha giocata una. La scelta di questi quattro eventi condizionanti
è data dal fatto che ci è piuttosto facile calcolare le
probabilità condizionate in questi quattro casi:
-
se la carta giocata da S apparteneva a un gruppo
di quattro, evidentemente E non può avere in mano nessuna carta
dello stesso valore, quindi
P(B|A4) = 0; -
se S ha in mano tre carte di un certo valore, nel
mazzo ne rimane soltanto un’altra. Tra tutti i modi in cui a E
possono arrivare dieci delle trenta carte che rimangono nel mazzo, allora,
sono “favorevoli” soltanto quelli in cui gli capita quella carta e nove
qualsiasi delle rimanenti ventinove: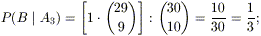
-
se S ha in mano due carte di un certo valore, nel
mazzo ne rimangono altre due. Gli unici casi in cui nessuna di queste due
capita a E sono quelli in cui E ha ricevuto dieci delle altre
ventotto carte: indicando allora con Bc l’evento “B
complementare”, cioè l’evento in cui E non ha in mano la carta
del valore giusto, si ha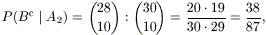
quindi
P(B|A2) = 1 – P(Bc|A2) = 49 / 87; -
infine, se S gioca una carta “singola”, e quindi
in “in giro” ci sono tre carte dello stesso valore, ragionando come sopra si
può concludere che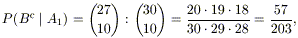
quindi
P(B|A1) = 1 – P(Bc|A1) = 146 / 203.
Conosciamo allora tutte le probabilità condizionate
alla dimensione del “gruppo” a cui apparteneva la carta giocata da S.
Notiamo che, come era ragionevole supporre anche a priori, la
probabilità di fare scopa è tanto minore quanto maggiore
è la dimensione del gruppo di partenza (infatti
1 / 3 ~ 33%, 49 / 87 ~ 56% e
146 / 203 ~ 72%).
Purtroppo, però,
i nostri problemi sono ancora ben lontani dall’essere risolti. Per conoscere
la probabilità totale, infatti, è necessario conoscere la
probabilità degli eventi condizionanti; inoltre, per conoscere queste
probabilità, è necessario conoscere la linea di condotta di
S. Mi spiego con un esempio: supponiamo che all’apertura S
abbia in mano, tra l’altro, tre assi e due fanti. Che carta decide di
giocare? Potrebbe farsi forte del fatto che giocando l’asso darebbe la scopa
soltanto in un caso su tre e che oltretutto creerebbe una situazione
probabilmente interessante per il suo compagno; potrebbe però anche
scegliere la strategia (raccomandata dai giocatori di scopone e, in questo
caso, fortificata dal detto veneto per cui “fanti e cavài no sbaglia
mai”) di giocare il fante.
Abbiamo insomma scoperto
il punto sul quale mi sono concesso di sorvolare (come sempre, barando un
po’) in precedenza: avere in mano una carta non significa volerla giocare.
Prima il problema era di facile soluzione: se E è un giocatore
di scopone e ha la possibilità di fare scopa, si suppone che la
faccia. Questo ci fa permesso di identificare l’evento “fare scopa” con
l’evento “avere le carte buone per fare scopa”. Ora, invece, non possiamo
procedere fino a che non decidiamo quale debba essere la giusta condotta di
S sulla base delle carte che ha in mano. A questo scopo,
seguirò nel seguito la seguente linea di condotta per il primo
giocatore di mano (che è quella seguita, a quanto so, dai giocatori
“incalliti”, in base a considerazioni che farò in chiusura; trascuro i
semi delle carte, che pure hanno la loro importanza nel gioco):
-
se si hanno in mano quattro carte di uno stesso valore,
si gioca una di quelle quattro; -
se non si hanno in mano quattro carte di uno stesso
valore, ma si ha almeno una coppia, si gioca una delle due carte della
coppia; -
se non si hanno in mano nè coppie nè
“poker”, ma si ha almeno un “tris”, si gioca una delle carte del tris; -
se tutte le carte che si hanno in mano hanno lo stesso
valore, si butta un asso e si spera nella propria buona stella.
In questo modo possiamo capire a quali “mani” di S
corrispondono gli eventi Ai: A1 è
formato dalle mani che hanno tutte carte di valori diversi tra loro,
A2 dalle mani che hanno una coppia (e eventualmente qualche
tris) ma nessun poker, A3 dalle mani che non hanno
nè poker nè coppie ma hanno almeno un tris e
A4 dalle mani che hanno almeno un poker (e, eventualmente,
qualche tris e/o qualche coppia). Ci resta soltanto il compito di contarle
(e scusate se è poco).
-
È abbastanza facile capire quali sono le mani di
A1: sono i sottoinsiemi dell’insieme delle 40 carte che si
ottengono scegliendo una delle quattro possibili carte per ogni valore.
Allora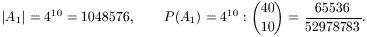
-
Contare le mani di A4 è meno
facile ma ancora fattibile. A una prima riflessione, si potrebbe pensare di
contarle scegliendo uno dei 10 possibili valori per il poker e prendere tutte
e quattro le carte di quel valore, aggiungendo poi sei qualsiasi delle altre
trentasei, cioè di scrivere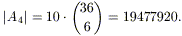
In questo modo, però si starebbero contando due
volte le (poche!) combinazioni che contengono due poker. Per ottenere il
numero giusto bisogna allora sottrarre dal totale ottenuto in precedenza il
numero di queste ultime combinazioni, e si ottiene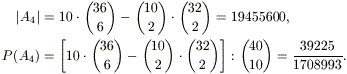
Cercando di contare in questo modo anche le mani di
A2, però, iniziano invece i veri problemi. Non
basta, infatti, scegliere uno dei 10 possibili valori per la coppia, prendere
due carte di quel valore e aggiungere otto qualsiasi delle altre 36: dobbiamo
infatti eliminare dal totale i casi in cui tra queste otto vi siano quattro
carte dello stesso valore (perché allora avremmo una mano con un
poker, già contata in precedenza). Inoltre, tra tutte le possibili
combinazioni che otteniamo in questo modo ce ne sarebbero alcune che
comprendono più di una coppia e che staremmo contando con una
molteplicità piuttosto laboriosa da calcolare. Va da sé che
questi problemi si ingigantirebbero in modo atroce quando dovessimo contare
gli elementi di A3.
Conviene allora passare
a un metodo un po’ meno “teorico” e “elegante” ma certamente più
efficace, anche in considerazione del fatto che fornisce risultati facilmente
applicabili a altre “strategie” di gioco della prima carta:
-
determiniamo tutte le possibili distribuzioni che
possono venire assunte da una mano di carte; -
contiamo tutti i possibili modi in cui ognuna di queste
distribuzioni può essere realizzata.
Se anche questo metodo può sembrare più
laborioso del precedente, vedremo che con l’aiuto di un po’ di malizia (e
magari di un buon foglio di calcolo!) riusciremo a raggiungere i risultati
che ci interessano in modo abbastanza spedito.
Per determinare quante
configurazioni possono assumere dieci carte scelte da un mazzo di quaranta
(uguali per valore a quattro a quattro), conviene iniziare dal caso
più eclatante, cioè quello in cui si abbia il maggior numero
possibile delle combinazioni più lunghe possibile. Si tratta,
evidentemente, del caso in cui abbiamo due poker e una coppia, cioè le
carte si raggruppano per valore secondo lo schema AAAA BBBB CC.
C’è anche un altro modo in cui possiamo avere due poker, ovvero il
caso in cui le altre due carte sono di due valori diversi
(AAAA BBBB C D). Esclusi questi, non potremo avere in mano
più di un poker, e quindi iniziamo a considerare le mani che ne hanno
esattamente uno. Iniziamo ancora da quella con le carte combinate nel modo
più “lungo” possibile, cioè da una mano con un poker e due tris
(AAAA BBB CCC), per poi proseguire in questo modo fino a arrivare
alla mano con le combinazioni più “corte” possibili, ovvero quella che
ha tutte e dieci le carte di dieci valori diversi
(A B C D E F G H I J). In
questo modo si determinano abbastanza facilmente tutte e 23 le possibili
configurazioni (invito il lettore a provarci prima di proseguire).
Fissata una
combinazione, il numero di modi in cui può essere realizzata si
può determinare come segue. Supponiamo di avere fissato una
combinazione con a poker, b tris, c coppie e d
carte “singole” (dove, evidentemente, deve essere
4a + 3b + 2c + d = 10).
Scegliamo i valori delle carte da associare a questa combinazione, iniziando
dagli a valori tra i dieci possibili con cui realizzare i poker.
Dovremo poi scegliere i b valori (tra i 10 – a
rimasti) con cui realizzare i tris e, quindi, i c valori (tra
10 – a – b) con cui realizzare le coppie e
i d valori (tra
10 – a – b – c) da dare
alle carte singole. Consideriamo poi che:
-
un poker di carte di un dato valore si può
realizzare soltanto in un modo: prendendo tutte e quattro le carte di quel
valore; -
un tris di carte di un dato valore può essere
effettuato scegliendo un seme da “lasciare fuori” dal tris, cioè in
quattro modi possibili; -
una coppia di carte di un dato valore può essere
realizzata scegliendo due qualsiasi delle quattro carte di quel valore; -
una carta singola di un certo valore può essere
scelta in quattro modi possibili.
Dovrebbe a questo punto essere facile convincersi che la
combinazione fissata può essere realizzata in
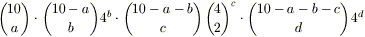
modi. Sulla base di questa formula, che può essere
semplificata nell’equivalente
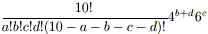
e/o automatizzata in un foglio di calcolo, è stata
realizzata la tabella che segue.
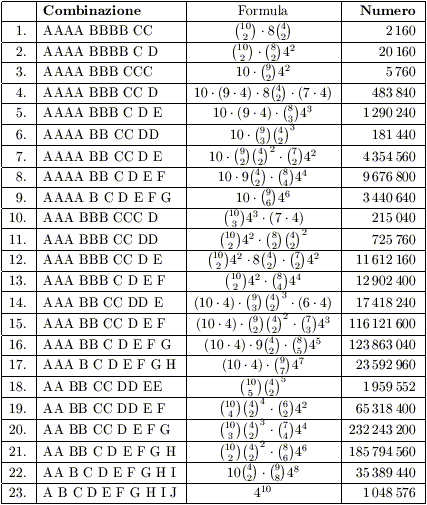
La tabella ci permette di calcolare quasi senza fatica il
numero di casi favorevoli a ognuno dei quattro eventi. È infatti
immediato vedere che:
-
A1 è formato dalle mani che
hanno combinazione come nell’ultima riga: allora
|A1| = 1 048 576 (come del resto
già trovato in precedenza); -
A2 è formato dalle mani con
combinazione come quelle delle righe 11., 12., 14., 15., 16., 18., 19., 20.,
21. e 22: sommando i valori presenti in tali righe si ottiene allora
|A2| = 790 445 952; -
A3 è formato dalle mani con
combinazione come quelle delle righe 10., 13. e 17, quindi
|A3| = 36 710 400; -
A4 è formato dalle mani le cui
combinazioni compaiono nelle prime 9 righe, quindi
|A4| = 19 455 600 (anche questo
già trovato in precedenza).
Per ricavare la “probabilità di fare scopa
all’apertura” (dove le virgolette sono motivate dalle ipotesi che abbiamo
fatto sulla condotta dei giocatori), allora, basta dividere i quattro valori
appena ottenuti per il numero totale delle possibili mani (che, per la
cronaca, è 847 660 528) e sostituire le probabilità
così ottenute nella formula delle probabilità totali vista
sopra. Il risultato finale è che la probabilità cercata
è pari a
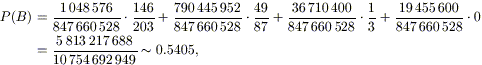
cioè la probabilità cercata è circa il
54.05%.
Il lettore un po’
smaliziato potrebbe chiedersi perché la condotta di gioco del primo
giocatore debba per forza essere quella proposta. Sembrerebbe infatti che,
nel caso in cui si abbiano in mano una coppia e un tris, sia meglio giocare
una delle carte del tris, perché in questo modo la probabilità
di concedere la scopa all’apertura dovrebbe diminuire sensibilmente. In
effetti, dare la precedenza ai tris sulle coppie “sposterebbe” dall’evento
A2 all’evento A3 le 269 740 800
mani corrispondenti alle combinazioni che si trovano nelle righe 11., 12.,
14., 15. e 16 e in questo modo si otterrebbe
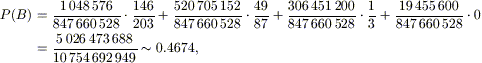
cioè circa il 46.74%, decisamente minore del
precedente. Dove sta l’inghippo? L’inghippo sta nel fatto che quando
E fa scopa su una carta di una coppia di S, esiste comunque una
probabilità significativa che la quarta carta di quel valore sia
posseduta dal compagno di S e, quindi, che non si concedano altre
scope oltre la prima. Questo invece non è più vero se S
gioca una carta di un tris: nel malaugurato caso in cui E riesca a
fare scopa, N (il compagno di S) si trova di nuovo nella
situazione di avere una probabilità attorno al 50% di lasciare una
scopa a O (il compagno di E). Ho insomma il sospetto (che
probabilmente potrebbe anche essere verificato da un lettore armato di buzzo
particolarmente buono, con un bel po’ di conti analoghi a quelli visti sopra)
che la strategia che ho esposto sopra, pur non minimizzando la
probabilità di lasciare la scopa all’apertura, renda tuttavia minimo
il valore atteso del numero di scope concesse consecutivamente
all’apertura. Se questo mio sospetto fosse vero, dato che tutti i
punti (non solo quelli fatti al primo scarto) sono ugualmente importanti, la
scelta della strategia di sopra sarebbe pienamente giustificata.