Nelle mie peregrinazioni in matematica, come turista, mi sono imbattuto in una vecchia conoscenza (tempi del liceo) che vorrei chiarire. Condizione necessaria: A si dice condizione necessaria per B se: La negazione di A(~A) è incompatibile con B Mio esempio (A= avere 4 lati , B= essere un quadrilatero) in questo caso non avere 4 lati è incompatibile con B. Condizione sufficiente: A si dice condizione sufficiente per B se: A è incompatibile con la negazione di B(~B) In questo caso avere 4 lati è incompatibile col non essere un quadrilatero Se al posto di quadrilatero metto quadrato le cose cambiano e la condizione diventa necessaria ma non sufficiente. Quindi vorrei sapere se quello che ho scritto ha una parvenza di chiarezza, se avete una formulazione diciamo più matematica , se quando una condizione al test è necessaria ed anche sufficiente si può usare quel famoso scioglilingua -> Condizione necessaria e sufficiente …..eccetera eccetera.

Matematica  ·  LogicaViews: 1856

Nel calcolo dei predicati, il concetto di implicazione
è così definito:

  • condizione sufficiente GÞ
    H     = NOT(G) OR H

ove H e G sono proposizioni che valgono
“Vero” o “Falso”:

Quindi, la proposizione “G implica H” è
vera se è vero il complemento di G oppure H.

Domanda: come è definita la condizione necessaria,
in termini degli operatori booleani ?

Proviamo a rispondere alla domanda analizzando il concetto
di implicazione ed il relativo significato di condizione necessaria/sufficiente
da una prospettiva differente.

La domanda posta dal lettore mi fa venire in mente una
discussione che ebbi con un carissimo amico qualche tempo fa. Discutevamo
delle cattive abitudini di guida dei proprietari di un certo tipo di autovettura,
piccola e scattante, a cui daremo il nome di fantasia “Fart”. Il
centro della discussione era proprio sul significato logico della mia
affermazione:

tutte le persone che non rispettano
il codice stradale guidano la Fart [1]

il mio amico sosteneva, offeso, che io fossi ingiusto
con tutta la categoria dei possessori di Fart.

La sua argomentazione principale consisteva nel sostenere
di possedere la Fart e di rispettare in ogni caso il codice della strada.
La mia replica era di non aver mai affermato che chi guida la Fart non
rispetta il codice stradale.

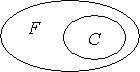
Fig. 1

La figura 1 descrive in modo grafico la configurazione
degli insiemi F, dei guidatori di Fart e C dei criminali
che non rispettano il codice della strada, rispetto all’affermazione,
o più propriamente proposizione, [1] .

Dire, ammetto un pò categoricamente, che chi non
rispetta il codice stradale guida la Fart equivale ad affermare l’assioma
tra gli insiemi C ed F che segue:

tutti gli elementi in C sono anche elementi
in F

ovvero che l’insieme C è strettamente contenuto
in F.

Esistono, quindi, elementi di F non contenuti in
C, ovvero persone che guidano la Fart pur rispettando il codice
stradale. Ciò significa affermare che essere un criminale è
una condizione sufficiente per guidare una Fart. Viceversa, il
guidare una Fart non è condizione sufficiente per non rispettare
il codice stradale.

Inoltre, avendo detto che l’insieme C è
strettamente contenuto in F, ciò vuol dire che tutti
i criminali che non rispettano il codice della strada guidano una Fart
e, quindi, che non vi sono criminali che guidino altre vetture. Ciò
significa affermare che guidare una Fart è una condizione necessaria
per essere un criminale.

Passando ad una rappresentazione più formale, abbiamo
visto le seguenti relazioni, mutuamente equivalenti, tra gli elementi
c dell’insieme C e gli elementi f dell’insieme F.

  1. Appartenere a C è condizione sufficiente di
    appartenenza ad F:     “
    c    Î C Þ
    c     Î F
  2. Appartenere ad F è condizione necessaria di
    appartenenza a C:     $
    f    Î F t.c.
    f     Î C

Le due affermazioni, illustrate graficamente dalla Fig.
1, sono equivalenti. Infatti, dire che

  1. C Þ
    F     (C implica F, C è
    condizione sufficiente per F) ovvero C     Ì
    F
  2. F Ü
    C     (F è implicata da C,
    F è condizione necessaria per C)

    3. equivale ad affermare la stessa cosa. Entrambe le preposizioni
    rappresentano lo stesso fatto, visto dai due versi dell’implicazione.
    Ma ciò che è interessante notare è la definizione
    di condizione necessaria, come azione di “essere implicato da”, e condizione
    sufficiente, come azione dell’”implicare”.

    Una terzo tipo di implicazione è l’unione delle
    due, ovvero il concetto di condizione necessaria e sufficiente:

  3. C Û
    F     (C implica F e F implica
    C, F è condizione necessaria e sufficiente per
    C e viceversa)

Analizziamo questa relazione:

  • Tutti gli elementi di C sono anche elementi di
    F : C     Ì
    F
  • Tutti gli elementi di F sono elementi di C
    : F     Ì
    C

da cui segue che

  • F = C

Riassumiamo le assunzioni fatte:

  • abbiamo definito due proprietà, “guidare una
    Fart” ed “essere un criminale”
  • abbiamo associato a queste due proprietà gli
    insiemi F e C, rispettivamente
  • abbiamo associato il concetto di “implicazione” (condizione
    sufficiente    ) all’appartenenza ai due insiemi, definendo la relazione
    che segue: C     Þ
    F     : cÎ
    C     Þ c Î
    F,     ovvero C Ì
    F    .
  • e quindi il suo opposto verso (condizione necessaria):
    C     Ü
    F     : fÎ
    F     Þ f Î
    C,     ovvero C É
    F    .
  • infine l’unione dei due (condizione necessaria e
    sufficiente    ): C     Û
    F     : fÎ
    F     Û f Î
    C,     ovvero C = F.

 

Possiamo quindi rispondere alla domanda ricordando che
la condizione necessaria è definita come verso opposto di implicazione
della condizione sufficiente:

  • G è condizione necessaria per H,
    ovvero G    Ü
    H , ovvero H    Þ
    G     = NOT(H) OR G

Infine, scriviamo l’espressione booleana della condizione
necessaria e sufficiente, ottenuta unendo le definizioni viste:

  • condizione necessaria e sufficiente GÛ
    H     = (NOT(G) OR H) AND (NOT(H)
    OR G ) = NOT(G XOR H)

Vedi una risposta precedente