Il calcolo proposizionale è il procedimento mediante
il quale si deducono, mediante regole formali ben definite, proposizioni
da altre proposizioni. Le operazioni utilizzate sono quelle dell’algebra
booleana convenzionale: OR (somma logica), AND (prodotto logico),
NOT, XOR.
Definizione
G(X1,…,Xn) : {T,F}
x … x {T,F} 
{T,F}
è una proposizione di arità n con parametri
gli atomi X1,…,Xn
Una proposizione è una espressione che può
valere vero o falso, ed è esprimibile in termini
di linguaggio informale, come ad esempio mediante la frase “socrate
è mortale“, o con un formalismo matematico corrispondente,
come nella formula proposizionale mortale(socrate)= vero. Entrambe
le espressioni hanno lo stesso significato.
Nel calcolo proposizionale, una formula proposizionale
è una espressione G composta da atomi, unità
logiche che possono valere vero (T, dall’inglese “true”)
o falso (F, dall’inglese “false”).
L’insieme {T,F} è detto
spazio booleano.
Si dice atomo una variabile booleana X
{T,F},
il numero di atomi o parametri booleani che definiscono una proposizione
è detto arità della proposizione.
Un literal L è una variabile booleana
ottenuta negando o meno un atomo.
L’assegnazione di valori agli atomi che compongono la
definizione è detta interpretazione della formula proposizionale.
Una proposizione è in forma normale congiuntiva
se è definita come prodotto logico di literal, mentre viene detta
in forma normale disgiuntiva se espressa come somma logica di literal.
Definizione
G è tautologia 
G(X1,…,Xn)=T
(X1,…,Xn)
{T,F} x
… x {T,F}
G è contraddizione G(X1,…,Xn)=F
(X1,…,Xn)
{T,F} x
… x {T,F}
ovvero G è detta tautologia se e
solo se è identicamente vera per ogni sua interpretazione; viceversa,
G è detta contraddizione se e solo se è identicamente
falsa per ogni sua interpretazione.
Le operazioni formali che consentono di dedurre
una proposizione G da una H sono le seguenti:
- G
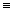H (equivalenza)
G = H per ogni interpretazione
di G, H - G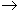H (implicazione)
NOT(G) OR H
= T - G
H
(condizione necessaria e sufficiente)
NOT(G XOR H)
Il teorema fondamentale del calcolo proposizionale è
il seguente.
Teorema (Principio di Deduzione)
Siano F1,…,Fn , G proposizioni,
F1 AND … AND Fn
G F1
AND … AND Fn AND NOT(G) è
una contraddizione
ovvero, G è conseguenza logica del
prodotto logico delle proposizioni Fi se e solo se il
prodotto logico delle proposizoni Fi e della proposizione
G è identicamente falso per ogni interpretazione degli atomi
che lo compongono.
Una estensione del calcolo proposizionale è il
calcolo dei predicati, costruito in base alla logica del primo
ordine.
Le differenze sostanziali tra calcolo dei predicati e
calcolo proposizionale sono le seguenti:
- Un atomo può essere una variabile booleana,
una costante o una proposizione. - La definizione dei quantificatori esistenziale
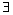
(esiste) ed universale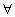(per
ogni).
Tutti i concetti di interpretazione, tautologia, contraddizione
e deduzione sono analoghi a quelli del calcolo proposizionale.
Il calcolo dei predicati, il cui linguaggio di programmazione
d’elezione è il Prolog, consente di definire proposizoni
su delle costanti, variabili o proposizioni e, quindi, di trattare espressioni
logiche complesse.
Ad esempio, è possibile descrivere la proposizione
X è cugino di Y mediante una espressione tipo
cugino(X,Y):=zio(A, X) . padre(A,Y)
ove l’operatore ‘.’ indica prodotto logico e l’operatore
‘:=’ è di definizione.
Questa espressione calcola la veridicità dell’espressione
X è cugino di Y (di gradi vari) verificando l’esistenza
di un elemento A che sia contemporaneamente padre di X e
zio di Y.
Perché una proposizione sia interpretabile occorre
che sia definita, vale a dire che, se per uno dei literal che la compongono
non esiste definizione, allora il predicato è indefinito.
Supponiamo, ad esempio, di definire le seguenti clausole
costanti (o fatti):
zio(adolfo, barbara) . – i.e. “Adolfo è
lo zio di Barbara”
padre(adolfo, claudio). – i.e. “Adolfo è
il padre di Claudio”
una clausola costante è una interpretazione del
predicato per cui questo sia vero, vale a dire, se G è un
predicato e a, b sono costanti:
G(a,b). G(a,b)
= T
Alla luce di queste affermazioni, il predicato
cugino(claudio,barbara):= zio(adolfo,barbara).padre(adolfo,
claudio) = T.T = T
è verificato, ovvero è una tautologia
per la sua unica interpretazione possibile.
D’altro canto, il predicato cugino(claudio, davide)
non è né vero, né falso, ma indefinito, per via della
mancanza di informazioni necessarie ad ottenere una interpretazione valida
per esso.
Utilizzando il Prolog, è possibile interrogare
la macchina con una clausola del tipo
cugino(X, barbara).
a cui il sistema risponde con
X = claudio
Il meccanismo che consente alla macchina di fare tanto
sfoggio di intelligenza è basato su un algoritmo di unificazione,
che opera per sostituzioni ed unificazioni di prodotti logici di predicati.
Questo procedimento è stato costruito grazie all’importantissimo
risultato di Herbrand pubblicato nel 1930 con un teorema omonimo.
Il Teorema di Herbrand fornisce infatti una metodologia
per confutare (i.e. rendere inconsistenti) le proposizioni. Un teorema
è essenzialmente una proposizione che utilizza le operazioni di
implicazione () e condizione
necessaria e sufficiente ()
che, abbiamo visto, sono riconducibili alle operazioni booleane
- G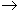H =
NOT(G) OR H - GH
= NOT(G XOR H)
Se l’algoritmo di confutazione fallisce, allora è
stata trovata una dimostrazione del teorema.
Rispondendo al lettore, quindi, possiamo dire che una
dimostrazione è una catena di deduzioni e sostituzioni ed un procedimento
automatico di dimostrazione di un teorema può consistere nel confutarne
la negazione mediante il teorema di Herbrand. In questo senso, se alcuni
assiomi necessari alla dimostrazione non vengono esplicitati, il teorema
non è dimostrabile vero ne dimostrabile falso, ma rimane indefinito.