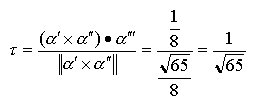Il raggio di curvatura di una curva nel piano/spazio in un punto è definito come il raggio della circonferenza, detta cerchio osculatore, che meglio approssima la curva in quel punto.
Per comprendere questo concetto con un esempio visivo, si immagini di percorrere con un’auto abbastanza veloce (e qui si aggiunga pure il lusso che si vuole) un tratto di strada in montagna, e si osservi la figura 1:
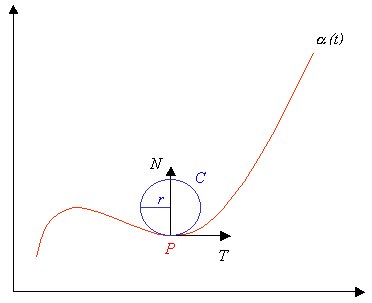
Fig 1: curva nel piano, vettori tangente, normale e cerchio osculatore in un suo punto P
la curva a nel piano tracciata in rosso rappresenta la strada che si sta percorrendo, il vettore T nel punto P, rappresenta la direzione della velocità del veicolo ed è detto tangente.
Ma cosa succede quando corriamo in curva con il nostro bel bolide fiammante? Avvertiamo distintamente un’accelerazione verso l’esterno della curva, a cui corrisponde un’accelerazione di verso contrario applicata ai pneumatici, detta accelerazione centripeta. Quest’accelerazione è provocata dalla forma della strada, dalla velocità del veicolo e dalla tenuta di strada dei pneumatici ed è tanto più intensa quanto più veloce percorriamo il tratto di curva. Il vettore N, quindi, rappresenta la direzione dell’accelerazione centripeta.
Il cerchio osculatore è la circonferenza tracciata in blu di figura 1, la migliore approssimazione della curva nel punto P, ed il raggio r è detto raggio di curvatura della curva a.
Raggio di curvatura ed accelerazione centripeta sono in relazione inversamente proporzionale, vale a dire che tanto minore è il raggio di curvatura e tanto più intensa è l’accelerazione centripeta, e viceversa.
La strumentazione del nostro bolide è in grado di fornire, col tachimetro, la velocità v del veicolo; se avessimo a disposizione un sensore in grado di determinare l’accelerazione centripeta del veicolo ac, ad esempio mediante un pendolo con filo a piombo, potremmo calcolare il raggio di curvatura della strada mediante la [1]
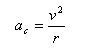[1]
da cui otterremmo r=v2/ac.
Nell’esempio mostrato, abbiamo introdotto delle misure fisiche (accelerazione, velocità) per determinare il raggio di curvatura. Ovviamente, esiste una metodologia più generale, che dobbiamo alla geometria differenziale, per calcolare parametri caratteristici di forma di curve e superfici nello spazio.
Il resto di questo articolo introduce il calcolo dei coefficienti di curvatura e torsione per curve tridimensionali, esponendo essenzialmente la metodologia e presentando i risultati principali. I risultati proposti sono il frutto di una trattazione piuttosto complessa, che non trova completo spazio in questa sede. L’autore resta a disposizione per ulteriori chiarimenti in merito.
Si presuppone una conoscenza apriori di:
¨ calcolo vettoriale
¨ calcolo delle derivate
Introduciamo brevemente la notazione standard utilizzata: siano x=(x1(t),…,x3(t)), y=(y1(t),…,y3(t)) vettori tridimensionali, diciamo
¨ norma di x: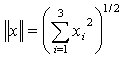 
¨ prodotto vettoriale di x, y: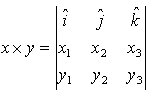 
ove i, j, k siano i tre versori delle coordinate cartesiane tridimensionali
¨ prodotto scalare di x, y: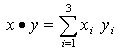 
¨ derivata prima, seconda e terza di x: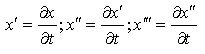 
¨ x è detto unitario se ||x|| = 1
Si consideri ora una curva nello spazio tridimensionale, espressa in funzione di un parametro t
come ad esempio l’elica cilindrica di Fig. 2
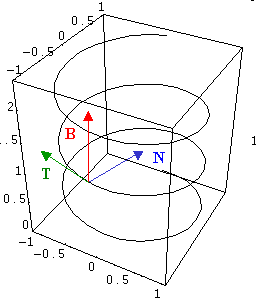
Fig 2: Elica cilindrica, vettori tangente, normale e binormale
determinata dall’equazione parametrica a(t) = (sin(t), cos(t), t/8).
I vettori mostrati T, N, B in Fig. 2 sono detti, rispettivamente tangente, normale e binormale, ove il vettore tangente è congruente con la direzione del vettore velocità della curva a ed il vettore normale è ortogonale ad esso e punta in direzione del centro di curvatura di a. Il terzo vettore, B, indica la direzione ortogonale alle altre due, per questo è definito binormale, ed indica la direzione di torsione di a, cioè la direzione verso cui la curva tende a cambiare piano di appartenenza.
Si immagini ora di costruire i campi vettoriali, T, N, B dei vettori (di lunghezza 1) tangenti, normali e binormali a tutti i punti della curva a. Vogliamo qui definire le caratteristiche di forma spaziali di una curva in termini dei campi vettoriali tangente, normale e binormale T, N, B e dei valori di curvatura e torsione k e t, rispettivamente.
Nel caso bidimensionale abbiamo visto che la curvatura dipende dalla velocità di percorrimento della curva, ma che significato ha parlare di velocità della curva a? Derivando la curva a rispetto al parametro t, otteniamo proprio il suo vettore velocità e l’intensità della velocità della curva è una funzione v del parametro t pari alla norma del vettore velocità
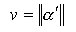[2]
Ad esempio, la velocità della curva di Fig. 2 ha un valore costante per ogni t, infatti:
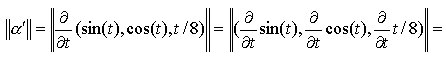
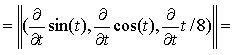
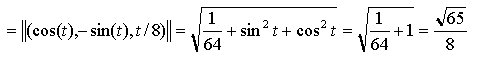
curve di questo genere vengono dette a velocità costante.
E’ nostro interesse determinare T, N, B unitari per applicarli come sistema di versori rispetto a cui le coordinate siano espresse unicamente in funzione della velocità della curva, della curvatura e della torsione.
Abbiamo detto che a’ esprime un campo tangente alla curva a, la cui intensità è pari a v, la velocità della curva in ogni punto. Il nostro scopo è, però, determinare T campo vettoriale unitario ma, per questo, è sufficiente normalizzare:
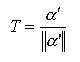[3]
e, sfruttando la [2] otteniamo
a‘ = vT [4]
Il parametro k, o curvatura, è definito nel modo seguente:
T’=kvN [5]
la dimostrazione della [5] è dovuta a Frenet.
Il legame tra curvatura e le derivate successive di a si ottiene dal prodotto vettoriale tra le derivate prima e seconda di a:
[6]
ottenuta applicando la [5] ed osservando che il prodotto vettoriale di un vettore per se stesso è sempre nullo (TxT=0) ed il campo vettoriale binormale è proprio definito come prodotto vettoriale degli altri due (TxN=B)
Calcoliamo ora la norma della [6]:
[7]
poiché B è unitario (||B||=1). Otteniamo quindi l’espressione della curvatura k:
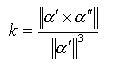[8]
e, dalla [6] del campo vettoriale binormale:
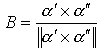[9]
e di quello normale, come prodotto vettoriale degli altri due:
[10]
Per quanto riguarda l’espressione della torsione, se ne omette la dimostrazione (perché artificiosa, ma senza difficoltà concettuali)
t = (a’ x a”) • a”’ / || a’ x a”||2 [11]
Infine, si dimostra che la relazione tra raggio di curvatura r e coefficiente di curvatura k è
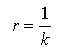[12]
relazione che consente di scrivere l’equazione della curva passante per i centri di curvatura
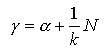[13]
Applichiamo ora le formule viste nel caso della spirale cilindrica di Fig. 2:
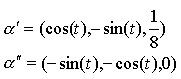
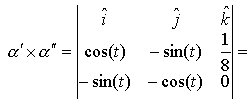
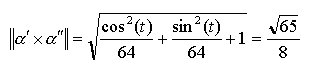
da cui otteniamo la curvatura
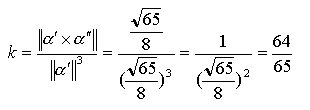
e la torsione
