La determinazione della condizione di esistenza di una
equazione generica serve ad assicurarsi che
l’equazione non perda di significato assumendo
valori indefiniti o infiniti.
Le condizioni da verificare sono essenzialmente tre:
- Il denominatore non deve essere nullo
- Gli argomenti delle radici di ordine pari devono
essere non negativi - Le funzioni componenti devono essere definite
Nel caso delle funzioni trigonometriche, coinvolte
nelle equazioni goniometriche, occorre assicurarsi che
queste non assumano valori nulli al denominatore.
Si considerino i grafici delle funzioni
seno, coseno e tangente in figura 1, 2 e 3.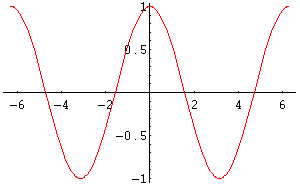
Fig. 1: Grafico di sen(x)
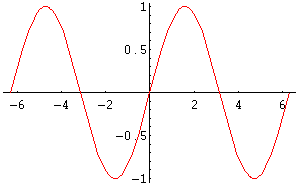
Fig.2: Grafico di cos(x)
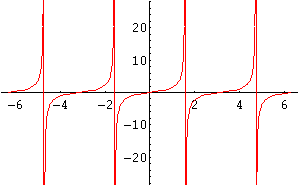
Fig. 3: Grafico di tan(x)
La funzione tan(x), definita come rapporto
tan(x) = sen(x)/cos(x)
assume valori infiniti per cos(x) = 0, ovvero
per ![]() .
.
Il campo di esistenza della funzione tan(x) è
definito, quindi mediante la condizione di esistenza
![]() ed esprime il campo di variabilità della x
ed esprime il campo di variabilità della x
per cui la funzione non perde di significato.
Ad esempio la condizione di esistenza
dell’equazione goniometrica (non elementare)
![]()
si ottiene, quindi, ponendo
![]()
e
![]()