Leonardo
“Pisano” Fibonacci
Fibonacci (Leonardo), detto Leonardo Pisano,
matematico italiano (Pisa 1175 circa – 1240 circa). Dopo
avere assimilato, durante numerosi viaggi, le conoscenze
matematiche del mondo arabo, pubblicò intorno al 1202 la
sua opera fondamentale, il Liber abaci, con cui si
propose di diffondere nel mondo scientifico occidentale
le regole di calcolo note agli Arabi, ovvero il sistema
decimale ad oggi in uso in Europa. Nato in Italia e
vissuto in Nord Africa, con i suoi numerosi viaggi a
fianco del padre ha avuto occasione di riconoscere i
vantaggi offerti dai sistemi matematici localmente in
uso.
Nel Liber Abaci (“Il Libro
dell’Abaco”), in cui Fibonacci espone i
fondamenti di algebra e matematica usati nei paesi Arabi,
un problema fornisce l’occasione per
l’introduzione della serie numerica che oggi porta
il nome del matematico pisano e che si riscontra in
numerosi esempi in natura. Tra questi,
l’approssimazione del Rapporto Aureo.
Fibonacci pubblica nel 1220 il Pratica Geometriae
(“La Pratica della Geometria”), in cui espone
esaustivamente concetti di geometria e trigonometria e,
nel 1225, il Liber Quadratorum (“Il Libro dei
Quadrati”) in cui espone un metodo per approssimare
le radici quadrate e cubiche con una precisione di nove
cifre.
[S] La serie di
Fibonacci
La serie di Fibonacci è una successione di interi
definita a partire dalla coppia 1, 1 in cui
l’elemento successivo è calcolato come somma degli
ultimi due.
Una definizione più formale è:
Fib(0) = 1
Fib(1) = 1
Fib(n) = Fib(n-1)+Fib(n-2) se n>1
si osservi che il valore della funzione Fib è
definito in termini della funzione stessa. Funzioni di
questo tipo sono dette ricorsive e vengono
definite da equazioni dette ricorrenti o alle
differenze.
Proviamo a calcolare i primi numeri della serie a
partire dalla definizione informale, in cui costruiamo
l’elemento successivo per somma degli ultimi due,
iniziando dalla coppia 1, 1:
1 (primo numero iniziale)
1 (secondo numero iniziale)
2 = 1+ 1 (somma degli ultimi due)
3 = 2 +1 ( …. come sopra … )
5 = 3 + 2
8 = 5 + 3 ( …. come sopra … )
…
Applichiamo invece la definizione ricorsiva per
calcolare Fib(4), ovvero il quinto elemento
della successione (osservazione: il primo elemento è Fib(0)
)
Fib(4)
=
Fib(3) + Fib(2)
=
Fib(2)+Fib(1) + Fib(1) + Fib(0)
=
Fib(1) + Fib(0) + 1 + 1 + 1
=
1 + 1 + 1 + 1 + 1
=
5
Si osservi anche che la definizione ricorsiva, sebbene
più compatta, è computazionalmente svantaggiosa
rispetto alla definizione informale, presentata in forma
iterativa. In altri termini, il calcolo dell’n-mo
elemento della successione genera un albero di
computazioni dell’ordine del quadrato di n.
Ciò significa che per calcolare Fib(4) abbiamo
impiegato circa sedici operazioni.
Col metodo esplicito l’ordine delle computazioni
è di n, in quanto per calcolare Fib(n) dobbiamo
generare tutti e soli i valori degli elementi precedenti.
Il vantaggio della formulazione mediante equazioni
alle ricorrenze consiste nella facoltà di trovare, con
un metodo generalizzato per le equazioni alle ricorrenze
(brevemente esposto nel seguito), una formulazione
esplicita per il valore di Fib(n):
![]()
ove ![]() è il valore del Rapporto Aureo,
è il valore del Rapporto Aureo,
pari a
![]()
Si osservi che la formula esplicita proposta è
semplificata, producendo una serie di Fibonacci a partire
dalla coppia 0, 1.
[S] Natura, Estetica e
numeri di Fibonacci
Gli esempi in natura di elementi che richiamano la
serie di Fibonacci sono numerosissimi. La serie di
Fibonacci approssima il numero di placche che si contano
procedendo per circonferenze, a partire dalla base in un
frutto di ananas, analoghi esempi valgono per le pigne, i
lati della banana, la struttura dei grappoli d’uva
eccetera.
Tuttavia, l’esempio più eclatante è dato dalla
connessione con il Rapporto Aureo. Gli studi di Leonardo
Da Vinci sul corpo umano hanno indicato come Rapporto
Aureo il rapporto esteticamente più piacevole tra le
lunghezze del corpo umano (ad esempio tronco/gambe).
In un segmento, si fissi un punto intermedio in modo
che lo divida in parti diseguali. Le parti sono dette in
Rapporto Aureo se la parte più corta è proporzionata
alla più lunga allo stesso modo della parte lunga
rispetto all’intero segmento.
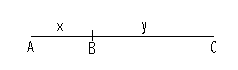
![]()
ovvero, supponendo che AB misuri x e BC
misuri y,
![]()
che definisce il Rapporto Aureo. Sostituendo alla
precedente
![]()
si ottiene
![]()
ovvero
![]()
da cui
![]()
da cui la determinazione della radice positiva perché
il rapporto è tra lunghezze di segmenti
![]()
Un rettangolo i cui lati siano in Rapporto Aureo è
detto Rettangolo Aureo. Esempi di Rettangolo Aureo sono
le carte in formato standard ISO, come Bancomat, carte di
credito, carte SIM per telefoni cellulari.
Il rapporto di due numeri consecutivi nella serie di
Fibonacci approssima il Rapporto Aureo, ad esempio:
8/5 = 1.6 ; 13/8 = 1.625; 21/13 = 1.615 …
più esattamente, il rapporto tra elementi successivi
della serie tende al Rapporto Aureo. Ciò significa che Fib(n+1)/Fib(n),
per n molto grande, assume un valore molto
prossimo a ![]() .
.
Rettangoli 8×5, 13×8, 21×13 sono, quindi, approssimazioni
via via più esatte di Rettangoli Aurei.
[U] Il calcolo della
formula esplicita
Si costruisce il vettore delle
condizioni iniziali
X0 = (1, 1)T
= (Fib(0), Fib(1))T
e si scrive l’equazione alle
ricorrenze in forma matriciale trovando la matrice A tale
che
(Fib(1), Fib(2))T
= X1 = A X0
da cui
![]()
poiché Fib(2) =Fib(1)+Fib(0) e
Fib(1) =Fib(1).
Gli autovalori di A sono ![]() e 1-
e 1-![]() ( ove
( ove ![]() è il Rapporto Aureo), quindi la matrice P
è il Rapporto Aureo), quindi la matrice P
che diagonalizza A è
![]()
a questo punto si calcola agevolmente Xn=(Fib(n),
Fib(n+1))T da
![]()
Da cui
![]()
per Fib(0)=0 e Fib(1)=1.
Il rapporto tra due elementi successivi
converge a ![]() . Questo fatto si dimostra
. Questo fatto si dimostra
semplicemente calcolando
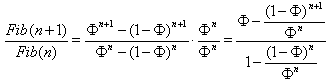
e passando al limite,
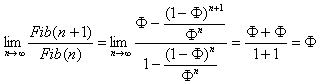
Per un po’ di
storia sul rapporto aureo propongo il sito: