La scienza opinabile ? Sicuro come 2+2 = 4 !
Anni addietro, da studente del corso di laurea in Scienze dell’Informazione, quando mi accingevo a studiare la computabilità degli algoritmi, rimasi letteralmente folgorato dal
Teorema di Incompletezza di Godel
"Per ogni sistema formale di regole ed assiomi è possibile arrivare a proposizioni indecidibili, usando gli assiomi dello stesso sistema formale"
perché, assieme al
Principio di Indeterminazione di Heisenberg
"Non possiamo mai conoscere contemporaneamente e con precisione la posizione e la quantità di moto di una particella subatomica"
postulava la inconoscibilità dell’universo, demoliva la fede nell’assolutismo razionalistico su cui avevo basato praticamente tutta la mia scala di valori: un razionalismo positivista incentrato sulla certezza che un’accurata osservazione potesse penetrare nel midollo del cosmo fino a comprenderne l’essenza strutturale e, soprattutto, sulla certezza assoluta che nulla fosse inconoscibile e tale da sfuggire alla comprensione dell’uomo.
Questo passo ha segnato, secondo la mia visione, il momento più importante della mia formazione scientifica. Al di là dei riflessi filosofici, la semplice coscienza che la scienza è astrazione di un modello su una realtà, mi ha reso protagonista consapevole dei risultati che mi accingevo a studiare, cosciente della loro natura umana, imperfetta e modificabile.
Ringrazio quindi il lettore, con cui concordo pienamente, per avermi dato la possibilità di discutere su questi due importanti risultati del nostro secolo.
Avevo già affrontato parzialmente la questione nella prima risposta che ho scritto per ViaLattea [6]. La domanda era “lo zero appartiene ai numeri naturali ?” e la risposta è stata, in soldoni, “dipende”.
Per usare i termini del lettore, “ le pretese razionalistiche di una capacità assoluta
della ragione di conoscere e di cogliere mediante una certezza assoluta ”, sono caratteristiche di chi ha un atteggiamento demodé e, comunque, poco scientifico.
Ogni volta che sento affermare “la matematica non è un’opinione” rabbrividisco. Rabbrividisco perché si utilizzano argomenti assolutamente non scientifici per affermare ciò che a noi fa comodo, sotto l’aureo cappello della “scienza”. Frasi come “sicuro come 2+2=4” sono dannose e deleterie, perché diffondono un immagine della scienza (quella vera) del tutto distorta.
Non solo la matematica è un’opinione: è il più grande ed articolato, ma molto ben fondato, sistema di opinioni che l’uomo abbia mai prodotto e, come è tale, è discutibile, opinabile, modificabile e adattabile. Altrettanto vale per le scienze in generale.
Lo straordinario risultato di Godel dimostra addirittura che a dispetto di tutti gli sforzi possibili, qualsiasi sistema formale può produrre teoremi indecidibili (ovvero né veri, né falsi): l’uomo non è quindi in grado di produrre sistemi di rappresentazione, o modelli, “perfetti”.
Aggiungendo a questo che l’unico strumento che l’uomo ha a disposizione per conoscere l’universo è un sistema formale che lo modelli, poiché l’universo è inconoscibile con precisione (dal risultato di Heisenberg), si direbbe proprio che siamo costretti a rinunciare alle nostre pretese di assolutismo razionalistico.
Ad onor del vero, bisogna dire che nessuno scienziato o persona dotata di un certo background scientifico serio si sognerebbe mai di affermare che la scienza è in grado di comprendere e descrivere con certezza assoluta i fenomeni.
Questo atteggiamento è più proprio del senso comune che assegna valenza assoluta alle proprie percezioni. Per ignoranza, infatti, molte persone sono disposte a scommettere sulla veridicità di ciò che hanno visto o udito, oppure sulla univocità di significato delle proprie affermazioni.
Eppure anche il linguaggio, al pari di qualsiasi altro sistema formale o informale di rappresentazione, gode della stessa proprietà di incompletezza dimostrata da Godel.
Si rifletta sul significato dell’affermazione
“questa frase è falsa”
qual è il suo significato ? Se la frase è vera allora è vero che è falsa e, quindi, non può essere vera; se, invece, la frase è falsa allora è falso che la frase è falsa e quindi deve essere vera. La frase è semplicemente indecidibile, ovvero è sia falsa che vera e sia non-falsa che non-vera.
In ogni caso, abbiamo appurato che il nostro linguaggio è imperfetto e non ha potenziale espressivo sufficiente per descrivere situazioni come questa. Ma attenzione, perché tutti questi “casi limite” giacciono in un confine è in grado di indicare proprio la “vera” natura dell’universo.
Esistono configurazioni del cosmo in cui le cose sono sia vere che non vere ? E se esistono, siamo in grado di comprenderle e descriverle ?
Modelli, realtà e percezione
Gli scienziati sono perfettamente al corrente del fatto che stanno investigando delle proprietà di modelli della realtà, piuttosto che la realtà stessa. Le famose “teorie scientifiche” servono proprio a questo. Un modello diventa teoria quando è dimostrata la sua adattabilità “locale” ad un sottoinsieme di fenomeni oggetto dello studio.
Un concetto chiave da introdurre immediatamente è l’isomorfismo: diciamo che due gruppi di oggetti sono isomorfi se esiste una corrispondenza uno-a-uno tra gli oggetti che li compongono. Il termine isomorfo proviene dal greco e significa “stessa forma” o “stessa struttura”.
Così, una teoria che dimostri l’esistenza di un isomorfismo tra il modello prodotto e la realtà di riferimento è considerata valida.
La figura 1 illustra le relazioni tra teoria, modello e realtà.
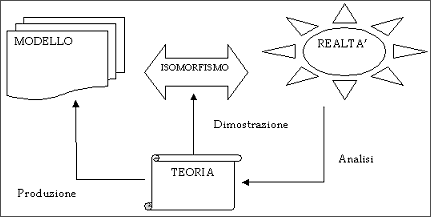
Fig. 1: Relazioni tra teorie scientifiche, modelli e realtà di riferimento
Lo scienziato analizza la realtà che vuole modellare e ingloba tutti i risultati ed i dati estratti dalle proprie osservazioni all’interno della teoria che sta sviluppando. La teoria ha come scopo la produzione di un modello matematico della realtà analizzata. Nel lavoro di formulazione della teoria dimostra anche l’isomorfismo tra modello e realtà di riferimento.
Se il modello non è in grado di coprire alcuni aspetti della realtà, allora la teoria viene estesa, fino a che è possibile coprire tutti i fenomeni che si vogliono investigare. Se l’isomorfismo non sussiste più, allora la teoria non è valida.
Nella realtà un lavoro di ricerca assurge a teoria solo quando l’isomorfismo è ampiamente dimostrato.
Un esempio di modello è l’equazione della gravitazione universale di Isaac Newton, nella sua Teoria della Gravità
![]()
con cui è possibile prevedere il moto degli oggetti nel cosmo, la loro posizione, velocità, ecc.
Trovare una soluzione ad un problema nel modello, in virtù dell’isomorfismo tra modello e realtà, significa quindi risolvere il problema nel mondo reale. Ma attenzione: nella fase di ricerca della soluzione l’oggetto della percezione umana non è la realtà, ma il modello.
Ciò avviene anche perché la realtà è inconoscibile ed in ogni modello si operano delle forzature o si ignorano relazioni di minore interesse all’interno della realtà di riferimento. Un esempio di semplificazione è l’equazione dei gas “ideali” in termodinamica:
PV = nRT
La rappresentazione di un fenomeno reale è quindi un problema percettivo legato al modello che si osserva. Per di più, la stessa osservazione è basata su un modello di rappresentazione costruito automaticamente dal nostro cervello durante l’osservazione.
Vale a dire che quando guardiamo il mare non abbiamo l’esperienza del mare vera e propria, ma stiamo analizzando i dati che arrivano al nostro cervello, codificati secondo un modello innato e diverso per tutte le persone.
Tutti noi, quindi, quando viviamo non sperimentiamo la vera essenza delle cose, ma il modello di riferimento. La percezione è, quindi, costituita dalla rappresentazione interna frutto della codifica dell’energia scambiata col mondo reale. In questo senso, la percezione non può avere valore assoluto, perché ha come oggetto dei dati codificati, non il mondo stesso.
La scienza è però in grado di rispondere alla domanda “che cosa significano le rappresentazioni all’interno del modello, nel mondo reale ?”. In termini più formali, qual è la semantica (significato) della percezione ?
Una parte fondamentale del lavoro di Godel è incentrata sulla dimostrazione di un isomorfismo tra le possibili percezioni/rappresentazioni ed i numeri naturali. Il processo di assegnare un intero ad una rappresentazione è detto Godelizzazione, che consiste essenzialmente nella possibilità di assegnare un numero univoco ad ogni sequenza di percezioni. Essendo il numero univoco, possiamo assegnare a questo numero il compito di definire il significato della percezione, ovvero la sua semantica. Dimostrato ciò, abbiamo assegnato un significato unico ed inscindibile ad una sequenza di percezioni. Se dico che il mio monitor ha numero di Godel 36973498573249, ogni volta che mi riferirò a questo numero, saprò di cosa sto parlando: del monitor, appunto.
L’affermazione di Godel ha effetti di proporzioni impressionanti: tutto è codificabile con semantica assegnata. Questo è il motivo per cui abbiamo la possibilità di trattare digitalmente immagini, suoni, filmati e tutte le entità per cui sia definito un apposito modello.
Tuttavia questo fatto non deve ingannare, perché è pur vero che possiamo Godelizzare praticamente ogni entità (comprese le teorie, i modelli, i programmi ed i programmi che Godelizzano entità), ma resta sempre l’incompletezza del sistema formale (Godel) che stabilisce il modello di acquisizione e l’impossibilità di una percezione della realtà indipendente dall’osservatore (Heisenberg).
Ma si rifletta un attimo: la semantica della rappresentazione al computer della immagine di un tramonto ha forse meno valore rappresentativo dell’immagine che si forma nella nostra mente ? Come possiamo allora affidarci alla nostra percezione come descrizione univoca della realtà e preferire questa ad altre ?
I due sistemi di rappresentazione, umano e digitale, hanno lo stesso valore perché sono isomorfi: si tratta, in sostanza, di due strutture di modelli assolutamente equivalenti.
Anatomia dell’(in)conoscibile
Il principio di indeterminazione di Heisenberg complica decisamente le cose. Ogni volta che tentiamo di indagare la realtà siamo costretti ad accettare queste limitazioni
· l’osservatore modifica il comportamento dell’osservato
· l’osservazione è necessariamente ristretta ad una porzione del fenomeno osservato
in definitiva, non esiste un osservatore ed un osservato, ma l’unione di entrambi e l’osservazione in se fornisce dati su una coppia inscindibile di elementi: lo stato dell’osservatore e lo stato dell’osservato.
L’unica possibilità che resta allo scienziato-osservatore è di formulare un modello “verosimile” della realtà in esame.
Inoltre, il sistema formale che descrive il modello della realtà oscilla tra questi due estremi:
· coerenza: tutti i teoremi formulabili sul modello del sistema devono essere decidibili
· completezza: tutti gli enunciati formulabili sono teoremi (in altri termini: il modello deve essere in grado di coprire tutte le esigenze di rappresentazione della realtà di riferimento)
il risultato di Godel implica che un sistema coerente perde in completezza ed un sistema completo perde in coerenza. Questa argomentazione è affrontata in dettaglio proprio nella risposta sull’appartenenza dello zero ai numeri naturali [6].
In particolare, i sistemi formali non sono in grado di descrivere se stessi coerentemente. Un esempio è la frase “questa frase è falsa”, in cui la frase tenta di decidere la qualità di se stessa. In particolare, ciò che devasta qualsiasi sistema formale è la negazione: affermare l’esistenza formale di un oggetto non-oggetto. Esempi di questo fatto sono, appunto, l’indecidibilità di una frase in cui si attesti che questa è una non-frase, o decidere se il numero zero (un numero che rappresenta una non-quantità) appartiene agli insiemi dei numeri (che rappresentano quantità).
Le implicazioni filosofiche di queste indecidibilità sono più vaste ed illuminanti di quanto si possa immaginare: si direbbe che questi “accidenti” indichino proprio la vera natura del cosmo: una commistione di essenza e non-essenza in eterno mutamento. Quando un sistema tenta di descrivere se stesso, significa che sta indagando sulla propria essenza con i propri stessi strumenti. Ed il risultato è puntualmente, qualsiasi sistema esso sia, che il sistema arriva a descriversi con teoremi sia veri che falsi, sia non-veri che non-falsi. O, in altri termini: sia in termini di essere che di non-essere, mai disgiunti e contemporaneamente presenti.
Sorprendentemente, le filosofie orientali sono arrivate a questo risultato già da decine di secoli.
Nello Shodoka, testo sacro del Buddhismo Zen, si afferma:
"Chi è non pensiero? Chi è non nato? Se il non-nato esiste realmente, non può neppure nascere" [4]
nella Bhagavadgita, testo sacro induista:
“Enuncerò ora quel conoscibile con la cui conoscenza s’ottiene ciò che è immortale: il Brahman senza inizio, supremo: lo si dice né essere né non-essere “ [3] XIII/12
nel Tao Te Ching, libro sacro taoista (sull’essere ed il non-essere):
“Ciò che essi hanno in comune, io lo chiamo il Mistero, il Mistero Supremo, la porta di tutti i prodigi” [5] I
All’inizio di questo secolo il lavoro della fisica quantistica ha svelato finalmente l’essenza oltre l’essere ed il non-essere: l’energia.
Si direbbe che l’energia sia l’essenza di tutte le cose, e che la struttura di essere e di non-essere sia solamente una qualità soggettiva assegnata dall’osservatore. L’energia è in eterno fluire e mutamento. La massa è energia, gli alberi, le case, la voce, gli odori, i concetti e tutto l’universo è energia. Io dico che quell’oggetto è una casa perché i miei sensi la vedono delimitata in un certo modo, dipendente dal modello di rappresentazione applicato dal mio cervello. La casa, in “realtà”, è una distribuzione di energia nel cosmo. E l’energia si manifesta in elementi dalla natura duale, sia di particella che ondulatoria.
Il principio di Heisenberg stabilisce che è impossibile determinare univocamente e con precisione posizione e quantità di moto delle particelle e, in definitiva, che è impossibile osservare con “certezza assoluta” tutte le cose dell’universo.
E’ curioso osservare questa coincidenza lessicale: all’inizio del secolo Albert Einstein ha prodotto il modello dell’universo in termini di equazioni di campo, le cui soluzioni portano a diversi modelli di cosmogonia (i.e. di genesi dell’universo). E guardate un po’ come si esprime il Beato Signore, il cui corpo è l’universo stesso, nel tredicesimo canto della Bhagavadgita, in cui espone la Disciplina del conoscibile e del conoscitore:
“Questo corpo (…) è chiamato ‘il campo’. Colui che lo conosce, gli esperti della questione lo dichiarano ‘conoscitore del campo’ ” [4] XIII/1
noi, oggi, il conoscitore del campo lo chiamiamo fisico teorico.
Sono veramente lieto della domanda posta dal lettore, che indica una riflessione estremamente profonda ed importante. Inviterei caldamente il lettore ad approfondire questi temi. Una risposta veramente articolata alla questione sollevata può essere reperita in [1], in cui il lavoro di Godel è ampiamente discusso. Le interrelazioni tra fisica teorica e filosofie orientali sono invece ampiamente discusse in [2], ove si affrontano “a tutto tondo” i riflessi filosofici e scientifici del lavoro di Heisenberg.
In ogni caso, chiarite le enormi difficoltà concettuali da affrontare per tentare di conoscere il nostro universo, il lavoro fatto dalla scienza e dagli scienziati attraverso i secoli appare ancora più grandioso. Prendere atto della inconosciblità dell’universo non significa sminuire la validità del mondo scientifico: tutt’altro !
Il grande lavoro degli scienziati sta nel definire modelli le cui classi di isomorfismo con la realtà sono così ampie ed efficaci che, addirittura, sono isomorfe a qualsiasi altro modello che descriva gli stessi fenomeni.
Ciò significa che è possibile definire matematiche la cui aritmetica preveda che 2+2=5, ma queste sono tutte isomorfe alla nostra matematica. In questo senso, il valore della nostra matematica, pur se relativo, è immenso. Perché, pur essendo imperfetta, è altamente probabile che sia equivalente ad altre matematiche sviluppate in parti remote del cosmo.
Nel film “Contact”, lo scienziato Carl Segan ipotizza che una forma di contatto aliena possa mettersi in contatto proprio utilizzando sequenze di numeri primi: una ipotesi non del tutto assurda. Gli scienziati sono piuttosto confidenti nel fatto che qualsiasi altra matematica sviluppabile sia isomorfa alla nostra.
Paradossalmente, è proprio l’imprecisione che conferisce alla scienza il valore di linguaggio universale.
Vedi anche: un commento del prof. Piergiorgio Odifreddi.
Bibliografia e riferimenti
[1] D.R. Hofstadter, Godel, Escher e Bach: un’eterna ghirlanda fiorita, Adelphi
[3] Bhagavadgita (a cura di A.M. Esnoul), Adelphi
[4] Y.Daishi Il canto dell’immediato satori, Piccoli Saggi Mondadori
[5] Tao te Ching (a cura di J.J.L. Duyvendak), Adelphi
[6] Risposta precedente su ViaLattea, sull’appartenenza dello zero ai numeri naturali