Sia c(t)=(t, f(t)) l’espressione parametrica di
una curva continua in (a,b), vogliamo calcolare la sua lunghezza
approssimativa tra due punti a e b.
Dividiamo l’intervallo (a, b) in n sotto-intervalli
lunghi ![]() , come
, come
in Figura 1, e costruiamo le corde tra i punti della curva corrispondenti
agli estremi dei sottointervalli.
L’idea è di calcolare la lunghezza approssimata
della curva sommando segmenti successivi, come in figura 1.
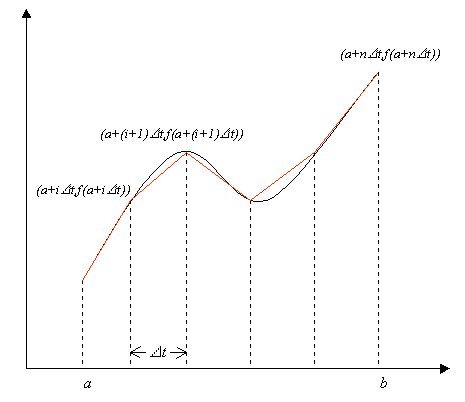
Fig. 1
Il metodo alle corde per il calcolo approssimativo della
lunghezza della curva di equazione c(t)=(t,f(t)), compresa tra
i punti a e b=a+n![]() t, consiste
t, consiste
nel calcolare la lunghezza della spezzata (composta dai segmenti in rosso)
di Fig. 1.
Ricordiamo che la lunghezza di un segmento nel piano di
estremi A=(a, b), B=(c,d) è espressa da
| [1] |
per cui, la lunghezza L della spezzata costruita
sulla curva c(t)=(t, f(t)) si ottiene da
| [2] |
Si osservi che al crescere di n, ovvero
del numero di intervalli di suddivisione, ![]() t
t
tende a zero e la curva è approssimata dalla spezzata sempre
con maggior precisione. Inoltre, il metodo è generalizzabile per
le curve ad un numero qualsiasi di dimensioni.