Peano, frattali e
mostruosità matematiche
Giuseppe Peano (Cuneo,
1858 – Torino, 1932) scoprì, nel 1890, una curva in
grado di riempire il piano “senza buchi”. La
curva di Peano ha scosso il mondo matematico tanto che
Hilbert definì le curve costruite in modo analogo
“Curve Mostruose”.
Lo sconcerto è
comprensibile, perché curve come quella di Peano
mappano, in modo ricorsivo, con uniforme continuità
segmenti in aree del piano.
Il procedimento
ricorsivo è definito partendo da un elemento di base
come quello definito in figura 1
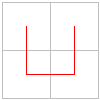
Fig. 1
Elemento Base
Nel passo successivo, la
figura viene costruita replicando per quattro volte
l’elemento base riducendone le dimensioni a un
quarto delle originali, mantenendo inalterato
l’orientamento delle due copie inferiori e ruotando
di 90 gradi a sinistra e a destra le due copie superiori.
Inoltre, effettuano le connessioni come da figura 2 (le
connessioni sono evidenziate in nero)
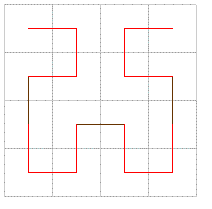
Fig. 2
Seconda Iterazione
(Il lato del quadrato ha
dimensione costante pari ad 1, le figure hanno dimensioni
crescenti solo per chiarezza)
La figura 3 illustra il
terzo passo dell’iterazione, che consiste nel
replicare quattro volte la figura del passo precedente,
ridotta di un fattore 4, applicando le operazioni di
rotazione e di connessione definite.
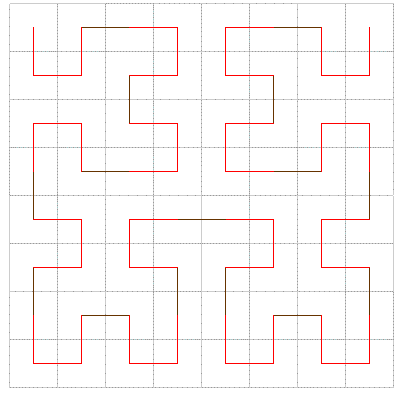
Fig. 3
Terza Iterazione
Iterando
all’infinito, si ottiene una “curva
limite” che copre interamente l’area a
disposizione.
Si osservi che ogni
iterazione suddivide il quadrato originario in quadrati
di dimensioni più piccole, contenenti repliche in scala
della curva del passo base. Questa proprietà è tipica
delle curve “frattali”, di cui possiamo trovare
ottimi esempi in natura (i profili delle coste, la
struttura dei fiocchi di neve, la geometria del fogliame
…).
Definizione della curva di
Peano
Definiamo ora
formalmente il processo di costruzione per induzione
strutturale della curva di Peano.
Mostreremo come la curva
di Peano è ottenibile come limite di una successione di
funzioni convergente.
La curva di Peano è
definita ricorsivamente mediante trasformazioni
successive di una curva f1
definita sul segmento [0,1] con valori nel
quadrato unitario Q0=[0,1]x[0,1]:
![]()
che descrive, ad
esempio, una curva come quella di figura 1.
Supponiamo ora di
dividere il quadrato unitario in quattro quadrati di lato
¼ Q00, Q01, Q10, Q11, come da figura 4.
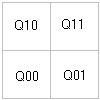
Fig. 4
Suddivisioni del quadrato unitario al secondo passo
Si costruisce la curva f2
del passo successivo modificando la curva
iniziale in modo che mappi [0,1/4] in Q00, [1/4,1/2]
in Q01, [1/2, ¾] in Q10 e in [3/4,
1]in Q11. Inoltre, occorre modificare la curva
tenendo conto delle rotazioni e dei segmenti addizionali
di connessione.
In ogni caso, la
funzione f2 sara definita
in modo tale che
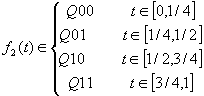
La larghezza degli
intervalli quadrati in questo passo (n=2) è paria ¼ ;
per induzione strutturale la larghezza degli intervalli
quadrati (o “sottoquadrati”) al passo
successivo (n=3) sarà 1/8 ed al passo n sarà 2-n..
In ogni passo si ripete
la divisione in quattro intervalli più piccoli e si
applicano le trasformazioni descritte al paragrafo
precedente.
Al passo n,
quindi, si ottiene una funzione che mappa il segemento
unitario al quadrato unitario
![]()
la curva di Peano si
ottiene per induzione iterando all’infinito il
procedimento esposto.
Convergenza, continuità e
suriettività
Mostriamo ora che la
successione fn converge
ad una funzione continua e suriettiva.
La cosa più
interessante da notare, è che, per il meccanismo di
sostituzione definito, la distanza massima i punti delle
curve fn ed fn+1
sono sicuramente contenuti nello stesso sottoquadrato di
ordine n, ovvero possono giacere ad una distanza
massima pari alla diagonale del sottoquadrato di ordine n
(il cui lato misura 2-n). Ciò significa
che,
![]()
Ora, applichiamo la
disuguaglianza nota come disuguaglianza triangolare
|x+y+z|<|x|+|y|+|z|
qui nella formulazione
stretta perché gli elementi sono tutti positivi.
Troviamo quindi una
minorazione per |fn+m(t)-fn(t)|
introducendo l’artificio di aggiungere e sotrarre le
funzioni di ordine intermedio tra n ed n+m,
ovvero:
|fn+m(t)-fn(t)|
= |fn+m(t)- fn+m-1(t)+
fn+m-1(t) … -fn+1(t)+
fn+1(t) –fn(t)|<
e applichiamo la
disuguaglianza triangolare
<|fn+m(t)-
fn+m-1(t)|+ … + |fn+1(t)
–fn(t)|< 21/2-(n+m-1)+
…+ 21/2-(n+1)+ 21/2-n
<
fattorizzando 21/2-n otteniamo
<![]() <21/2-n2=23/2-n
<21/2-n2=23/2-n
poiché i termini della
sommatoria di m elementi forniscono un
coefficiente moltiplicativo sicuramente non superiore a
2.
Ora una successione ai,
soddisfa il criterio di convergenza di Cauchy
se le differenze
|an+m-am|
convergono a zero, al
crescere di n ed indipendentemente da m.
Quini, la successione di
funzioni f0…fn
converge perché soddisfa il criterio di Cauchy.
Inoltre, la convergenza
è unforme perché vale per ogni t in [0,1]
e le singole funzioni fi sono continue,
per costruzione.
Le successioni dotate di
uniforme convergenza godono della importante proprietà
una successione di
funzioni continue/derivabili uniformemente convergente,
converge ad una funzione continua/derivabile.
Quindi, la funzione
limite della successione fi che
descrive la curva di Peano f(t)=![]() è continua.
è continua.
Inoltre, la funzione f(t)
è suriettiva poiché per ogni punto (x,y)
nell’intervallo quadrato [0,1]x[0,1], è
possibile determinare un valore del parametro t0
tale che la successione di valori fi(t0)
è via via più vicina alla coppia selezionata o,
più formalmente,
![]()
Questo risultato si
ottiene osservando che per ogni coppia (x,y) la
curva di ordine n passa sicuramente
all’interno del sottoquadrato di ordine n che
la contiene, ovvero la coppia dista dalla curva
sicuramente meno della diagonale del sottoquadrato,
ovvero:
|(x,y)-fn(t0)|<21/2-n
ma il limite per n
tendente all’infinito di questa espressione è,
appunto, zero. Ciò garantisce che
f([0,1])=[0,1]x[0,1]
e la funzione f(t)
è suriettiva.
Links (in inglese)
Definizione e proprietà
della curva di Peano
http://www.cut-the-knot.com/do_you_know/hilbert.html
Giuseppe Peano
http://www-groups.dcs.st-andrews.ac.uk/~history/Mathematicians/Peano.html
Esempio di curva di
Peano
http://www-math.uni-paderborn.de/~fazekas/course/peano.html
“Mostruosità”
matematiche
http://nova.stu.rpi.edu/~slattd/domain/monstrosities.htm
Tutorial sulla geometria
frattale
http://www.ccinet.com/~rob/fractal/what.html