La dimostrazione dell’irrazionalità di ![]() ” src=”../../esperti/mat/pi-greco/img1.gif”/> è piuttosto facile per chiunque ha studiato un po’ di calcolo.
” src=”../../esperti/mat/pi-greco/img1.gif”/> è piuttosto facile per chiunque ha studiato un po’ di calcolo.
Chiaramente per un ragazzo di 14 anni può essere difficile. Il mio
consiglio è di avere un po’ di pazienza ed aspettare di aver studiato
almeno qualcosa riguardo a derivate ed integrali prima di voler leggere
questa dimostrazione. Puoi trovare quanto ti serve nel capitolo ![]() ” src=”../../esperti/mat/pi-greco/img2.gif”/> del libro
” src=”../../esperti/mat/pi-greco/img2.gif”/> del libro
“Che cos’è la matematica?” di Richard Courant e Herbert
Robbins,
Bollati Boringhieri Editore.
La dimostrazione che ti propongo si trova invece nel capitolo 17 del
libro
“Introduction to Number Theory” di Hua Loo Keng,
Springer-Verlag, Berlin Heidelberg New York 1982
Teorema il numero ![]() ” src=”../../esperti/mat/pi-greco/img1.gif”/> è irrazionale.
” src=”../../esperti/mat/pi-greco/img1.gif”/> è irrazionale.
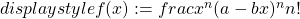 ” src=”../../esperti/mat/pi-greco/img6.gif”/>
” src=”../../esperti/mat/pi-greco/img6.gif”/> e
Osserviamo subito che sia ![]() ” src=”../../esperti/mat/pi-greco/img8.gif”/> sia le sue derivate sono numeri interi quando
” src=”../../esperti/mat/pi-greco/img8.gif”/> sia le sue derivate sono numeri interi quando ![]() ” src=”../../esperti/mat/pi-greco/img9.gif”/> o
” src=”../../esperti/mat/pi-greco/img9.gif”/> o ![]() ” src=”../../esperti/mat/pi-greco/img10.gif”/>, quindi anche
” src=”../../esperti/mat/pi-greco/img10.gif”/>, quindi anche ![]() ” src=”../../esperti/mat/pi-greco/img11.gif”/> e
” src=”../../esperti/mat/pi-greco/img11.gif”/> e ![]() ” src=”../../esperti/mat/pi-greco/img12.gif”/> sono due numeri interi. Con semplici calcoli si verifica che
” src=”../../esperti/mat/pi-greco/img12.gif”/> sono due numeri interi. Con semplici calcoli si verifica che
vale l’ugualianza
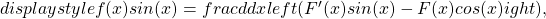 ” src=”../../esperti/mat/pi-greco/img13.gif”/>
” src=”../../esperti/mat/pi-greco/img13.gif”/>
dunque
è un numero intero. Ma, per ![]() ” src=”../../esperti/mat/pi-greco/img15.gif”/> e per
” src=”../../esperti/mat/pi-greco/img15.gif”/> e per ![]() ” src=”../../esperti/mat/pi-greco/img16.gif”/> sufficientemente grande, vale la seguente limitazione
” src=”../../esperti/mat/pi-greco/img16.gif”/> sufficientemente grande, vale la seguente limitazione
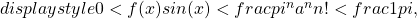 ” src=”../../esperti/mat/pi-greco/img17.gif”/>
” src=”../../esperti/mat/pi-greco/img17.gif”/>
quindi
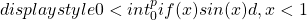 ” src=”../../esperti/mat/pi-greco/img18.gif”/>
” src=”../../esperti/mat/pi-greco/img18.gif”/> e dunque dalla (1) segue che ![]() ” src=”../../esperti/mat/pi-greco/img19.gif”/> non può essere un numero intero. La contraddizione
” src=”../../esperti/mat/pi-greco/img19.gif”/> non può essere un numero intero. La contraddizione
nasce dal fatto di aver supposto ![]() ” src=”../../esperti/mat/pi-greco/img1.gif”/> razionale, quindi la tesi è dimostrata.
” src=”../../esperti/mat/pi-greco/img1.gif”/> razionale, quindi la tesi è dimostrata.
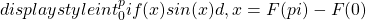 ” src=”../../esperti/mat/pi-greco/img14.gif”/>
” src=”../../esperti/mat/pi-greco/img14.gif”/>