Esiste una relazione tra il lato del
poligono regolare ed il raggio delle circonferenze
iscritta e circoscritta, qualsiasi sia il numero di lati.
Proviamo ad investigarla insieme.
Ad occhio, si osserva che un poligono è divisibile in
tanti triangoli isosceli uguali quanti sono i suoi lati;
inoltre, tanto maggiore è il numero dei lati del
poligono (5, nel caso del pentagono) tanto più acuto è
l’angolo al vertice di ogni triangolo. E’ evidente,
quindi, l’esistenza di una relazione tra l’ampiezza
dell’angolo al vertice e la lunghezza del lato del
triangolo.
Questa relazione è definita in modo preciso dalla
funzione trigonometrica seno dell’angolo al
vertice.
Ma cos’è una funzione trigonometrica ?
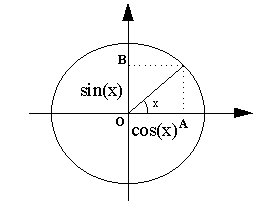
Fig. 1 – La circonferenza trigonometrica
Su una circonferenza di raggio 1, si
immagini di poter ruotare liberamente il raggio di un
angolo a piacere x.
Le proiezioni OB ed OA del raggio lungo gli assi di
figura 1 determinano le lunghezze delle funzioni seno e
coseno dell’angolo x, rispettivamente.
L’angolo x può essere misurato in gradi.
Ricordiamo che l’angolo giro misura 360 gradi.
Proviamo adesso a calcolare le funzioni trigonometriche
per qualche angolo.
Accediamo alla calcolatrice di Windows, e selezioniamo la
voce “Scientifica” dal menù
“Visualizza”. 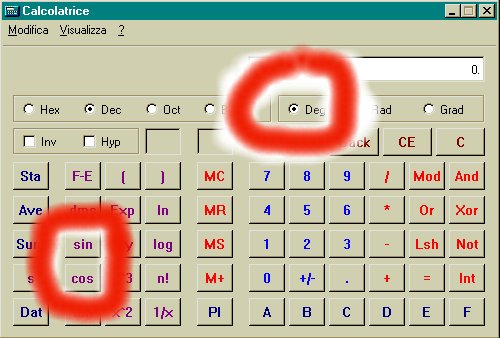 Fig. 2 – La calcolatrice scientifica di
Fig. 2 – La calcolatrice scientifica di
Windows
Innanzitutto, bisogna impostare la modalità di
misurazione degli angoli in gradi, selezionando
“Deg” e cliccando col mouse nell’apposita
casella.
Adesso, basta digitare una ampiezza in gradi e premere
uno dei tasti relativi alle funzioni seno (tasto
“sin”) e coseno (tasto “cos”). Ad
esempio, il seno di 60 gradi è uguale a 0.5 (un mezzo).
Osserviamo adesso un esagono regolare ed
inscriviamolo in una circonferenza.
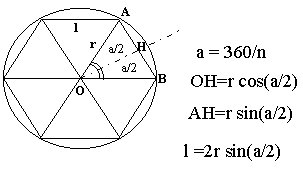
Fig. 3 – Esagono regolare e circonferenza circoscritta
L’esagono è costituito da sei triangoli isosceli (o
dovrei dire equilateri ? la risposta è per esercizio
…) il cui angolo al vertice a è di 360/6
= 60 gradi. Nella figura, n è uguale al
numero di lati, quindi n=6.
La lunghezza del lato dell’esagono è proporzionale
proprio al seno dell’angolo al vertice e, ovviamente,
alla lunghezza del raggio della circonferenza
circoscritta.
Osserviamo attentamente la figura 3.
Il triangolo OHA ha per angolo al vertice a/2 .
Confrontando con la fig. 1, osserviamo le seguenti
proprietà (supponiamo che r = 1):
- l’apotema OH dell’esagono è uguale al coseno
dell’angolo al vertice HOA - il raggio della circonferenza inscritta è uguale
all’apotema dell’esagono - il lato AB dell’esagono è uguale a due volte la
lunghezza del segmento AH, perché il triagolo
OAB è isoscele - il segmento AH è uguale al seno dell’angolo al
vertice HOA - la lunghezza del lato e dell’apotema dell’esagono
è proporzionale al raggio della circonferenza
circoscritta
Proviamo ad applicare le nostre osservazioni al caso
del pentagono, supponendo che il raggio della
circonferenza circoscritta sia uguale ad uno.
- il pentagono ha cinque lati, quindi n=5
- l’angolo al vertice a di ognuno dei
cinque triangoli isosceli misura 360/5
gradi. Quindi a = 72 gradi ed a/2
= 36 gradi - la lunghezza del lato del pentagono è quindi
uguale a 2 volte il seno di a/2 - usiamo la calcolatrice: il seno di a/2=36 gradi
è circa 0.5878 - moltiplichiamo per due il seno ed otteniamo la
lunghezza del lato del pentagono regolare: 1.176
Ciò significa che il lato del pentagono è uguale a
circa 1.176 il raggio della circonferenza
circoscritta. Inoltre, la misura del lato è
proporzionale a quella del raggio r, quindi se il
raggio vale 2, 3 ecc., il lato varrà 2×1.176, 3×1.176, e
così via.