Archimede di Siracusa, matematico e fisico greco (287
a.C. – 212 a.C.) ha studiato, presentandola in una opera dedicata alle
spirali (224 a.C.), la figura gemoetrica oggi nota come Spirale di
Archimede.
La spirale di Archimede è ottenuta tracciando una
circonferenza in modo continuo ed aumentandone il raggio in modo proporzionale
all’angolo percorso.
In coordinate polari, l’equazione della spirale di Archimede
è
r =aq
ove r
è la distanza dal punto tracciante all’origine degli
assi, q è
la distanza angolare percorsa ed a una costante a piacere.
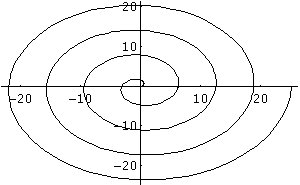
Fig. 1: Spirale di Archimede
La spirale di Fig. 1 è stata tracciata con Mathematica,
usando l’istruzione:
ParametricPlot[{t*Cos[t], t*Sin[t]}, {t, 0, 8 Pi}].
In geometria, la spirale di Archimede è utilizzata
per suddividere un angolo in tre parti uguali e per la quadratura del
cerchio. Un’interessante applicazione militare della spirale di Archimede
è nella tecnica di ricerca nel bosco: il plotone di ricerca parte
da un punto e si muove a spirale fino a coprire tutta l’area.