Approssimazione di funzioni tramite serie di
potenze
Il lavoro dei matematici Taylor e Maclaurin
ha prodotto un importantissimo metodo di approssimazione di funzioni in
serie di potenze, oggi largamente applicato nel calcolo numerico e nelle
moderne macchine calcolatrici elettroniche. Gli strumenti matematici che
consentono l’applicazione dei risultati di Taylor e Maclaurin si apprendono
in quinta liceo scientifico o nel primo anno di università, nelle
facoltà scientifiche. In questa sede verranno esposti i esclusivamente
i risultati.
Una serie di potenze è un polinomio di infiniti
termini della forma
![]() [1]
[1]
la serie di potenze in [1] è detta “centrata
in a” e i cn sono detti coefficienti
della serie di potenze.
Se esiste una serie di potenze che converge ad una funzione
f(x), allora la funzione è detta analitica. Ciò
implica l’esistenza di una funzione R(n) detta resto dell’espansione
parziale in serie di potenze
![]() [2]
[2]
in n termini. Se f(x) è analitica,
quindi, il resto R(n) converge a zero al crescere di n.
La formula di Taylor fornisce l’espressione dell’espansione
in serie di potenze di una funzione analitica f(x):
![]() [3]
[3]
la serie di potenze è detta di
Maclaurin se a=0 e l’espressione f(i)(x)
è la derivata di ordine i-mo della funzione f(x).
Approssimazione delle funzioni trigonometriche
L’approssimazione delle funzioni trigonometriche può
essere operata applicando quindi la serie di Maclaurin.
L’espansione polinomiale della funzione seno vale,
quindi,
![]() [4]
[4]
ed ha coefficienti unitari ma di segni alterni ed esponenti
dei termini dispari.
La figura 1 illustra graficamente le approssimazioni successive
per lunghezze crescenti dell’espansione polinomiale in serie di potenze.
della funzione seno. I numeri in rosso rappresentano il grado dell’espansione
polinomiale raffigurato.
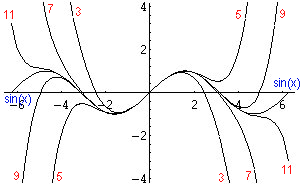
Fig.1: Espansione polinomiale della funzione
sin(x)
Si osservi come, al crescere della lunghezza dell’espansione
in serie, i polinomi approssimino con precisione crescente la funzione
seno.
Analogamente, la funzione coseno si approssima
con:
![]() [5]
[5]
e le approssimazioni delle altre funzioni trigonometriche
possono essere ricavate mediante l’applicazione della formula di Taylor
o sostituendo la [4] e la [5] nelle proprietà che le definiscono.
Note biografiche
Taylor (Brook), matematico inglese
(1685-1731). Nella sua opera principale, Methodus incrementorum directa
et inversa (1715), introdusse il calcolo delle differenze finite,
abbozzò la determinazione degli integrali singolari delle equazioni
differenziali e studiò i cambiamenti di variabili.
Maclaurin (Colin), matematico scozzese (Kilmoddan
1698 – Edimburgo 1746). Fu uno dei più insigni discepoli di Newton.
Si dedicò alla geometria pura, all’algebra e al calcolo infinitesimale
di cui sviluppò con genialità i princìpi. Nel suo
De linearum geometricarum proprietatibus generalibus tractatus,
oltre alla famosa formula che è nota ancora oggi con il nome di
formula di M., vi si trova trattato il problema dell’attrazione esercitata
da un ellissoide sopra un punto situato sulla sua superficie oppure interno
a essa e vi è rivelata la scoperta delle configurazioni sferoidali
d’equilibrio di una massa fluida omogenea soggetta a un moto rotatorio.
(fonte: Enciclopedia Multimediale Rizzoli ’98)