La differenza principale tra i metodi di calcolo FEM
(Finite Elements Method) e BEM (Boundary Element Method) sta
nel metodo di discretizzazione del dominio. I metodi BEM sono generalmente
migliori in termini di precisione ma sono applicabili in un numero ristretto
di casi.
Come giustamente il
lettore osserva, una trattazione completa richiede ampio spazio ed è al di
fuori degli scopi di questo articolo. Diamo quindi un cenno sul problema
generale e sulle caratteristiche principali dei due metodi, commentandone gli
ambiti applicativi e comparandone le caratteristiche.
Si supponga di voler modellare la dissipazione del calore su
una regione bidimensionale O come in figura:
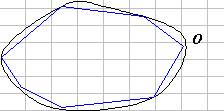
Si supponga che il calore sia distribuito nella regione
O secondo una funzione
u : R2 –> R che fornisca
i valori di temperatura in ogni punto (x, y) di O.
La discretizzazione della regione O, tracciata in
nero, è modellabile come segue:
- in superficie: come unione delle sottoregioni
Oij (i rettangoli in grigio); - al contorno: come unione dei segmenti oi
(in blu).
L’unione delle sottoregioni Oij
rappresenta quindi una discretizzazione della regione O mentre
l’unione dei segmenti oi rappresenta una discretizzazione
della frontiera o contorno di O, 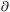 O.
O.
L’espressione della
dissipazione del calore, dato il coefficiente di dissipazione k,
costante nelle due dimensioni, è data dall’equazione di Laplace
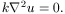
[1]
Il metodo numerico di calcolo della soluzione dell’equazione
di Laplace FEM consiste nel calcolo dell’integrale soluzione, date le
condizioni al contorno 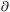 O,
O,
seguente:
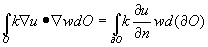
[2]
ove n è il vettore normale al contorno 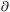 O e w è una funzione peso
O e w è una funzione peso
appositamente scelta.
Al di là dei
dettagli che portano alla soluzione della [1], ottenuta integrando per parti
dopo aver applicato il teorema di Gauss-Green, ciò che è
importante evidenziare è che il metodo FEM comporta la risoluzione
della [2] in ogni sotto-intervallo Oij, infatti la
caratteristica dei metodi FEM è quella di operare sulla
discretizzazione dell’intero dominio.
La soluzione
dell’equazione [2] discretizzata porta alla formulazione di un’equazione
matriciale la cui risoluzione fornisce i valori numerici della funzione
u(x, y), nei singoli sotto-intervalli
Oij.
Nel caso applicativo
generico (es.: diffusione acustica, di calore, di torsione, ecc.), il metodo
FEM è caratterizzato dalle seguenti proprietà:
- Richiede una discretizzazione dell’intero dominio, preservando
l’ordine dimensionale del problema (cioè, un problema nello spazio 3D
richiede calcoli integrali in R3). - La soluzione ricavata è valida per l’intero dominio.
- La soluzione ricavata è approssimata e l’approssimazione
peggiora al contorno. - La matrice generata è sparsa e simmetrica; la soluzione
del problema è quindi ricavabile mediante algoritmi estremamente veloci
ed efficienti. - Gli integrali che portano alla formulazione matriciale sono
generalmente semplici. - È generalmente applicabile, anche in problemi non lineari.
- È relativamente semplice da implementare.
Il metodo numerico di calcolo della soluzione dell’equazione
di Laplace BEM si poggia sulla definizione di una soluzione
fondamentale della [1], una funzione peso w per la definizione
degli elementi al contorno, soluzione della seguente:
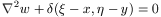
[3]
ove 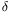 è la
è la
funzione di Dirac, singolare in 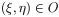 .
.
Esiste un elenco di soluzioni fondamentali note per varie equazioni e
relative classi di problemi, ma non è sempre possibile ricavarne una.
L’adozione della funzione di Dirac, insieme con
l’applicazione del teorema di Gauss-Green, consente di riscrivere la [2] in
termini del solo contorno 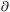 O:
O:
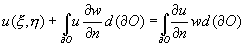
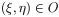 . [4]
. [4]La differenza tra i due metodi è proprio in questo
fatto: il metodo BEM opera su una discretizzazione della frontiera o
contorno del dominio. La [4] viene quindi risolta per i singoli
sotto-intervalli oi del contorno, in modo analogo al caso
FEM.
Si osservi che
ciò comporta la riduzione di una dimensione: nel caso specifico, la
frontiera è monodimensionale mentre il dominio è a due
dimensioni.
Nel caso applicativo
generico, il metodo BEM è caratterizzato dalle seguenti proprietà:
- Opera sulla discretizzazione del contorno, abbassando di
una dimensione i termini del problema (cioè, se il dominio
è a 3 dimensioni, le equazioni sono in R2).
Tuttavia, alcune superfici al contorno, specialmente se 3D, sono
particolarmente complesse da modellare. - È orientata al calcolo delle soluzioni al
contorno, le soluzioni in punti qualsiasi del dominio vengono calcolate
successivamente. I metodi BEM sono indicati quando si intendono
modellare fenomeni in punti particolari del contorno (es. resistenza
aerodinamica su un flap in estensione) o su regioni del dominio di
particolare interesse. - Le soluzioni sono approssimate solo al contorno, la
soluzione esatta nel dominio è infatti garantita dalla soluzione
fondamentale. - La matrice generata è generalmente popolata in
quasi tutti gli elementi, il calcolo della soluzione può essere
computazionalmente molto pesante. - Gli integrali sono particolarmente complessi e possono contenere
singolarità in grado di aumentare la complessità
dell’algoritmo numerico adottato per il calcolo e di abbassare contemporaneamente
l’accuratezza della soluzione numerica. - Richiedendo l’esistenza di una soluzione fondamentale,
può non essere applicabile persino per problemi lineari. - L’implementazione è notevolmente più
complessa, a causa della presenza di integrandi contenenti
singolarità.
Fonte: Hunter, Pullan, FEM BEM
Notes, University of Auckland, 2002.