solo 1 e n stesso. La divisione per qualsiasi altro numero naturale da’
un resto diverso da 0.
La successione dei numeri prima inizia cosi’:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29 , 31, 37 (e fino a mille continua
cosi’)
dipende dal significato che si da’ al termine “ordine”. Parlando in
senso generale, in questo contesto intendo la frase “trovare un ordine”
come “trovare una qualche proprieta’ interessante” nella successione
(oltre ovviamente a quella di essere numeri primi, che e’ la
definizione stessa della successione).
quanti ce ne sono. E’ intuitivo (e si puo’ dimostrare rigorosamente)
che mano a mano che nella successione degli interi i numeri diventano
piu’ grandi, si trovano meno numeri primi tra di essi, in quanto e’
piu’ facile che un numero molto grande possa essere diviso senza resto
da un numero piu’ piccolo. In linea di principio, sarebbe potuto
accadere che oltre un certo punto non ci fossero piu’ numeri primi,
ma che tutti i numeri fossero divisibili per altri piu’ piccoli. Invece
le cose non stanno in questo modo: comunque si scelga un numero, esiste
un numero primo piu’ grande, ossia esistono infiniti numeri primi. E
(sebbene sia una cosa facile da dimostrare e nota sin
dall’antichita’) si tratta di una proprieta’ “non banale”, perche’ vuol
dire che esistono dei numeri grandi quanto si vuole, che non possono
essere divisi per nessun intero piu’ piccolo!
generico numero primo oppure a sapere come sono distribuiti i numeri
primi tra gli interi.
il settimo e’ 14. E’ facile dimostrare che la formula per sapere qual
e’ l’n-esimo numero pari e’ 2n.
grande matematico Eulero, dopo aver tentato inutilmente di trovare tale
formula, scrisse di “gettare un’occhiata alle tavole dei numeri primi.
Ci accorgeremmo che non vi regna ne’ ordine ne’ legge”, ed in effetti
guardando queste tavole non
si puo’ non dargli ragione: il ritmo e’ irregolare, varia tra il raro ed il frequente in maniera apparentemente randomica.
Per esempio nella decade 307-317 ci sono ben 4 primi (307, 311, 313, 317) mentre
per avere i successivi 4 bisogna “attendere” ben 3 decadi (317, 331,
337, 347).
improvvisamente quando qualcuno scopre che guardando le cose da un
punto di vista diverso, diviene evidente un nesso tra due campi della
conoscenza apparentemente lontani tra loro. Il cambio di prospettiva
inizio’ a delinearsi nella mente di Gauss, probabilmente nel 1791
quando – quattordicenne – ricevette in dono un libro di logaritmi. In
quel tempo le tavole logaritmiche erano abbastanza diffuse tra i
mercanti perche’ erano utili a rendere piu’ veloci le operazioni di
moltiplicazione dei numeri (mercanzie x prezzo).
(ed anche nella domanda che ho posto sopra sull’esistenza di una
“formula”) e si era cercato di trovare il valore di ciascun numero
primo, ci si era fissati sul singolo. Gauss, invece, si focalizzo’
sull’insieme. Spesso nella scienza l’abilita’ e’ nel porre la domanda
“giusta” e la domanda in questione, piuttosto di quella riportata sopra
(“qual e’ l’n-esimo numero primo”) fu: “quanti numeri primi ci sono tra
1 ed N?” Da questa prospettiva per Gauss fu relativamente facile, con
un ragionamento statistico (visto l’aspetto casuale descritto sopra),
trovare una risposta approssimata alla domanda, ossia: N/log(N).
sui logaritmi, dichiarando: “non avete idea di quanta poesia ci sia in
una tavola dei logaritmi“.
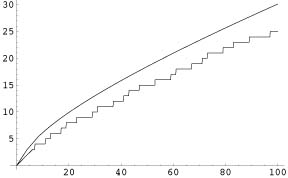
La stima di Gauss confrontata con il valore l’esatto di primi fino a 100
In seguito Gauss miglioro’ la sua stima, sempre basandosi
sull’apparente casualita’ della successione, ed anche questa stima piu’
complicata si fondava sul logaritmo. Ma si dovettero aspettare decenni
(ossia sino al 1859) per avere un altro significativo passo in avanti
nella comprensione della successione dei numeri primi. Tale passo fu
compiuto da Riemann e fu pubblicato (parzialmente) in un saggio di 10
pagine. Il passo di Riemann e’ un nuovo ed ancora piu’ radicale cambio
di prospettiva i cui dettagli non possono essere approfonditi ora (si
veda per esempio qui).
Riemann trovo’ dei nessi impressionanti tra lo studio di funzioni
continue di variabili complesse e somma delle serie, in particolare di
Fourier (questi nessi stavano delineandosi in quegli anni anche grazie
ad altri matematici) ed i numeri primi! In particolare Riemann mostro’
che si potrebbe calcolare la posizione dei numeri primi studiando
quando una speciale funzione (che prese il nome di zeta di Riemann) si
annulla. E’ sorprendente che l’irregolarita’ nella successione dei numeri primi, possa avere a che fare con le regolarita’ di una funzione
continua di variabile complessa! Ancora piu’ curioso e’ il fatto che
Riemann riesca a dimostrare che la formula statistica di Gauss puo’
derivarsi da una ipotesi di “ordine” sulla posizione degli zeri della
funzione zeta: l’apparente casualita’ dei numeri primi puo’ venir
generata dalla disposizione allineata degli zeri della funzione
complessa zeta! Ma tali zeri, sono effettivamente allineati? A
tutt’oggi ancora non e’ noto…
In realta’ affinche’ sia vera la formula di Gauss non e’
necessario che gli zeri siano effettivamente allineati, ma e’
sufficiente un’ipotesi piu’ debole, dimostrata indipendentemente da
Hadamard e Vallee-Poussine alla fine dell’ ‘800, circa cento (sic!)
anni dopo la formulazione dell’ipotesi di Gauss, che divento’ quindi il
Teorema dei Numeri Primi.
Come si vede di “ordine” nei numeri primi se n’e’ gia’ trovato ed allo
stato attuale il passo ulteriore sarebbe quello di dimostrare l’ipotesi
di Riemann. Tale dimostrazione potrebbe fornire un metodo che faciliti la scomposizione in fattori primi, che attualmente e’ difficile (ossia
richiede un tempo lungo, se vogliamo parlare dal punto di vista
computazionale), in quanto bisogna procedere a tentativi. Questa
difficolta’ e’ alla base di molti sistemi di sicurezza criptati (di cui vialattea si e’ gia occupata, vedi qui) che
dovrebbero essere modificati in caso si scopra tale “facilitazione”
(per la cronaca sistemi crittografici basati su altre tecniche sono
noti – ed in parte gia’ utilizzati).
Ma potrebbero esserci anche implicazioni piu’ profonde. Gia’ Gauss, nei
suoi appunti inediti, aveva trovato un nesso con l’idrodinamica di una
stella. Relazioni meno chiare sono state intuite con la fisica
quantistica dei nuclei atomici, con la teoria del caos, del caos
quantistico, con la struttura dei vetri ed addirittura con il
sequenziamento del DNA o con il calcolo delle probabilita’ che il
solitario Klondike riesca o fallisca! Allo stato attuale la maggior
parte di questi nessi sono ipotesi, ma in molti sperano che la
eventuale dimostrazione (se esiste!) del teorema di Riemann
possa far vedere nuova luce anche su questi campi, come e’ successo in
altri momenti storici (per esempio lo sviluppo della matematica delle
geometrie non euclidee ha consentito di sviluppare la teoria della
relativita’ generale).
La storia della ricerca di ordine nella sequenza dei numeri primi e’
affascinante, cosi’ come l’ingegno delle persone che ci si sono
dedicate. Ramanujan, per esempio, che – sebbene privo di educazione
matematica – fu in grado di scoprire indipendentemente i risultati di
Riemann. O Siegel che fu l’unico in grado di leggere alcuni caotici
manoscritti di Riemann, che rivelarono una formula incredibilmente
precisa per il calcolo degli zeri della “sua” zeta. Questa storia
appassionante, condita con aneddoti e vicende personali dei
protagonisti, e’ descritta in un libro che ho letto tempo fa e che mi
e’ molto piaciuto:
Marcus Du Sautoy L’enigma dei numeri primi Rizzoli, ISBN 88-17-00098-1