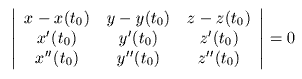Data una curva nello spazio R3, il cerchio osculatore alla curva in un suo punto P è quel cerchio che meglio approssima la curva attorno al punto P. Si tratta quindi di un’approssimazione del secondo ordine, in quanto al primo ordine la curva viene approssimata dalla sua retta tangente, oggetto lineare, mentre al secondo ordine si ottiene un’approssimazione più precisa, ovvero attraverso un arco di circonferenza.
Il cerchio osculatore è un oggetto piano, di conseguenza starà su un piano detto osculatore alla curva nel punto P. Il piano osculatore è il piano sopra il quale la curva tende a stare attorno a P, sebbene non ci stia veramente se la curva è sghemba. Per trovare la sue equazione basta scrivere la retta tangente alla curva in P, e considerare l’equazione del piano che passa per la tangente detta ed un altro punto Q della curva diverso da P; si ottiene una famiglia di piani dipendenti da Q. Passando al limite Q->P si trova, se esiste, l’equazione del piano osculatore. Detta x=x(t),y=y(t),z=z(t) la parametrizzazione della curva, sia t0 il parametro relativo al punto P; allora l’equazione del piano osculatore in p è data da
Su tale piano sta il cerchio osculatore, che viene definito come quel cerchio che ha come raggio il raggio di curvatura alla curva nel punto P, e centro sulla retta normale principale che sta anch’essa sul piano osculatore. Il raggio di curvatura è dato dall’inverso della curvatura, che è la rapidità con la quale cambia la retta tangente attorno al punto P. Per il calcolo, supponiamo di parametrizzare la curva mediante la sua lunghezza d’arco s; allora, detta γ la parametrizzazione, la curvatura risulta il modulo della variazione della tangente, ovvero c=|γ”(s)|. Si ha quindi R=raggio di curvatura=1/c, da cui il raggio del cerchio osculatore.