Il calcolo integrale è nato con
lo scopo di “quadrare” una funzione, ovvero di trovare l’area
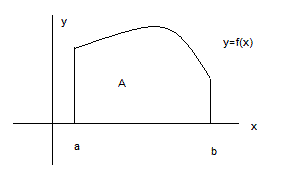
della regione di piano sottesa dal grafico della funzione, e da opportune rette verticali, in modo da rendere la regione limitata. Quadrare una funzione è un problema molto antico, ma solo nel 17° secolo si è trovata una soluzione analitica, data appunto dal calcolo integrale.
Se la funzione f ha, per esempio, andamento come nella figura seguente
allora per definizione, si ha
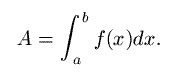
Dunque l’integrazione (secondo Riemann o Lebesgue) è un’operazione su funzioni che restituisce un numero reale, che, nel caso di funzioni positive di una sola variabile, è pari all’area della regione di piano delimitata dalla funzione e dall’asse x. Ne segue che il significato geometrico dell’integrale (definito) sta nella sua definizione.
Si dimostra solo in un secondo momento
che l’integrazione risulta essere l’operazione inversa della
derivazione.
A norma del Teorema fondamentale del calcolo integrale,
se f è una funzione continua in un punto x allora vale
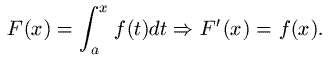
La definizione di
integrale è abbastanza complicata (vedi integrazione di
Riemann o di Lebesgue), mentre quella del Teorema citato è invece sufficientemente agevole.
E’ curioso notare che calcolo differenziale e
calcolo “integrale” (tale nome è stato dato solo a
scoperta avvenuta) si sono sviluppati inizialmente in maniera autonoma , e solo in seguito
si è scoperto che un’operazione è l’inversa dell’altra,
da cui l’appellativo “Teorema fondamentale del calcolo”.