Per arrivare ad una soluzione, seppur parziale, del problema è sufficiente tracciare un grafico della funzione f(x)=√(x2+k). Infatti, dopo uno studio rapido, si ha che f(0)=√k (supponiamo k>0) , f cresce per x>0, è convessa ed ammette come asintoto obliquo la retta di equazione y=x.
Il problema geometrico è quello di capire se il grafico di f incontra o no il reticolo nel primo quadrante formato da punti a coordinate intere. Qui di sotto è rappresentata una figura che rappresenta il caso k=2:
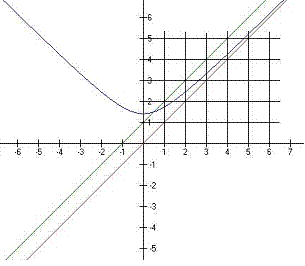
In tale grafico è rappresentata quindi la curva y=√(x2+2), e le rette y=x e y=x+1. Come si può notare il grafico non incontra mai il reticolo; quello che si può dire certamente, proprio per la presenza dell’asintoto obliquo y=x che attraversa il reticolo, è che il grafico di y=√(x2+k) non incontra il reticolo dei punti a coordinate intere dopo il punto di intersezione tra il grafico di f e la retta y=x+1. Dunque (dopo un rapido calcolo) possiamo dire con certezza che non esistono soluzioni intere se x>(k-1)/2.
Rimane aperta, in generale, la verifica per tutti i valori di x interi al di sotto della soglia (k-1)/2; sono comunque in numero finito, per cui è concepibile una verifica diretta, caso per caso.