La quadrica di equazione cartesiana x2-y2+z2=1 è un iperboloide iperbolico ad una falda, secondo la classificazione delle quadriche in forma canonica. Si tratta quindi di una superficie a punti reali, e non di una curva immaginaria.
Infatti, andiamo a trovare la forma quadratica associata, complessificando a lavorando nello spazio proiettivo complesso P3(C), ovvero R4– {0}/p, dove p è la relazione di equivalenza che identifica vettori proporzionali. La quadrica ha quindi equazione Q(v)=x12-x22+x32-x42=0, con v=(x1,x2,x3,x4). La matrice associata a tale forma quadratica, rispetto alla base canonica, è data da
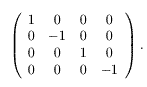
La forma quadratica è già in forma normale per poterne calcolare la segnatura, che quindi vale (2,2), dal momento che 2 è il numero di +1 (da cui il primo 2) e 2 =rango-2=4-2, poichè il determinante della matrice non è nullo. La segnatura è legata agli autovalori della matrice, ed è determinata univocamente da essi, per cui anche la segnatura di una forma quadratica è invariante rispetto a cambiamenti di base.