Semplificherò il problema, supponendo nulla la curvatura della terra; ritengo che sia sensato, in prima approssimazione, supporrè ciò dal momento che l’occhio umano non distingue nitidamente un oggetto ad una lontananza paragonabile alla cuvatura terrestre.
Per i conti successivi mi rifarò alla seguente figura:
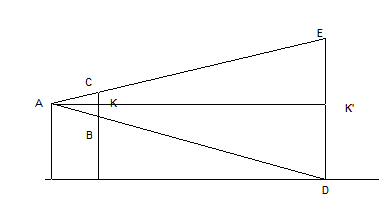
Il punto A denota l’occhio dell’osservatore, mentre il segmento DE denota la vera altezza della nave; il segmento BC denota invece l’altezza che l’occhio percepisce se posizioniamo un righello a distanza AK dal nostro occhio (ricordiamo posizionato in A). Allora per similitudine dei triangoli ABC e ADE si ha
BC/DE=AK/AK’.
Ne segue che AK’=DE*AK/BC.
Ad esempio, supponiamo di avere una nave alta 15m, e di posizionare un righello a 40 cm dall’occhio, leggendo 1cm di altezza della nave vista all’orizzonte; allora la nave dista 15*0,4/0,01 m=600m.