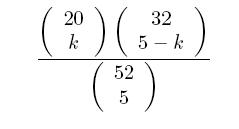L’evento favorevole è costituito da tutte le cinquine di carte contenenti almeno una tra quelle elencate. Bisogna dividere allora le carte in due categorie: quelle “fortunate” (ossia asso, k, q, j, 10) che sono 20, e le rimanenti “sfortunate” che sono 32.
Si può anche (e questo facilita la comprensione) ricondurre il tutto a uno schema d’urna: vi sono 52 palline, 20 delle quali “fortunate” e 32 “sfortunate”; dopo aver estratto 5 palline, si valuta la probabilità che ce ne sia almeno una fortunata.
Ci mettiamo in ipotesi di equiprobabilità degli eventi, ossia valutiamo la probabilità come rapporto (casi favorevoli)/(casi possibili).
Ovviamente la probabilità cercata sarà la somma delle probabilità dei seguenti eventi:
nella cinquina estratta c’è ESATTAMENTE UNA carta (pallina) favorevole; nella cinquina estratta ci sono ESATTAMENTE DUE carte (palline) favorevoli, e così via fino a cinque.
Ora la probabilità che, delle 5 carte (palline) estratte, ESATTAMENTE k siano favorevoli è
(questa formula costituisce il cosiddetto MODELLO IPERGEOMETRICO: esso prende il suo nome dal fatto che la funzione caratteristica di tale legge, cioè la trasformata di Fourier, è un’ipergeometrica confluente).
Per avere la risposta al quesito, somma tali probabilità per k da 1 a 5.