La cardinalità di un insieme non è una definizione ben data se l’insieme in questione non è finito. Nel caso generale quindi si parla solo di equipotenza tra insiemi, dicendo se due insiemi “hanno la stessa cardinalità” o no, ovvero se siano equipotenti oppure no.
Due insiemi A e B hanno la stessa cardinalità se esiste una funzione biiettiva f : A → B; moralmente stiamo dicendo che possiamo mettere in corrispondenza uno ad uno gli elementi di A con gli elementi di B.
Un fatto all’apparenza strano che può capitare è il seguente: A ha la stessa cardinalità di B, dove B è un sottoinsieme proprio di A, ovvero non coincide con A. E’ facile vedere, ed è molto intuitivo del resto, che questo fatto non può capitare se A è un insieme finito (il tutto è maggiore della parte come diceva Euclide), ma per gli insiemi infiniti invece è di regola. Basti pensare all’insieme N dei numeri naturali che è in corrispondenza biiettiva con il sottoinsieme proprio P dei numeri pari (f : N → P data da f(n)=2n).
Un intervallo in R ha ancora la stessa cardinalità di R, e questo mostra quanto richiesto; la seguente figura illustra quale sia la biiezione f che manda l’intervallo (x,y) sulla semiretta reale positiva, che ha la stessa cardinalità dell’intera retta reale:
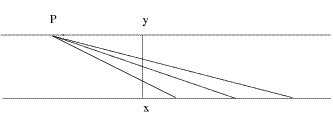
Quanto alla seconda parte della domanda, non è definita la cardinalità di una funzione; l’equipotenza è un concetto di tipo insiemistico, eventualmente si potrebbe parlare di cardinalità dell’insieme immagine della funzione data. Se questo fosse il quesito, allora è presto fatto: se la funzione f fosse costante oppure assumesse un numero finito o numerabile (in biiezione con N) di valori, allora l’immagine sarebbe finita o numerabile come insieme. Se la funzione f fosse invece continua e non costante su [a,b], allora per il Teorema dei valori intermedi l’immagine di f sarebbe un intervallo, chiuso e limitato per il Teorema di Weierestrass, e dunque un insieme che ha la stessa cardinalità di R.