Effettivamente, è di dubbio valore l'attribuzione a Pitagora del celebre teorema che porta il suo nome. Nonostante è ormai considerato certo che la proprietà enunciata dal teorema di Pitagora fosse sperimentalmente nota, almeno in alcuni casi particolari, anche da civlità preelleniche, pare che a Pitagora si debba quanto meno la prima dimostrazione: secondo Apollodoro il calcolatore Pitagora sacrificò un numero considerevole di buoi quando scoprì la famosa relazione tra i lati del generico triangolo rettangolo (D. Laerzio, Vite di filosofi, libro VIII, cap. 1). Se il sacrificio dei buoi è solo leggendario, la dimostrazione attribuita a Pitagora è invece storia. Essa è molto semplice e procede costruendo la seguente figura a partire dal triangolo rettangolo AFC.
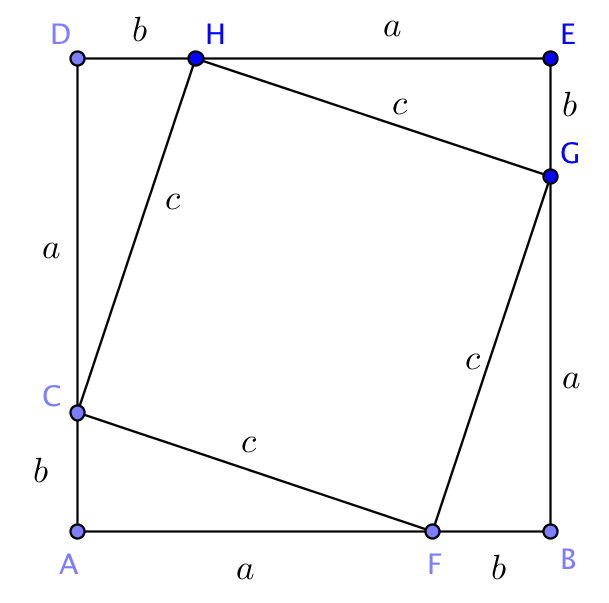
Una volta costruiti il quadrato ABED e CFGH ne viene per costruzione che (a+b)2=2ab+c2 ovvero a2+b2+2ab=2ab+c2 cioé a2+b2=c2. La dimostrazione che dà Euclide invece sembra che sia proprio opera personale, e si trova collocata come ultima proposizione del libro I degli Elementi, precisamente la proposizione 47. Illustriamola brevemente facendo riferimento alla figura che segue.
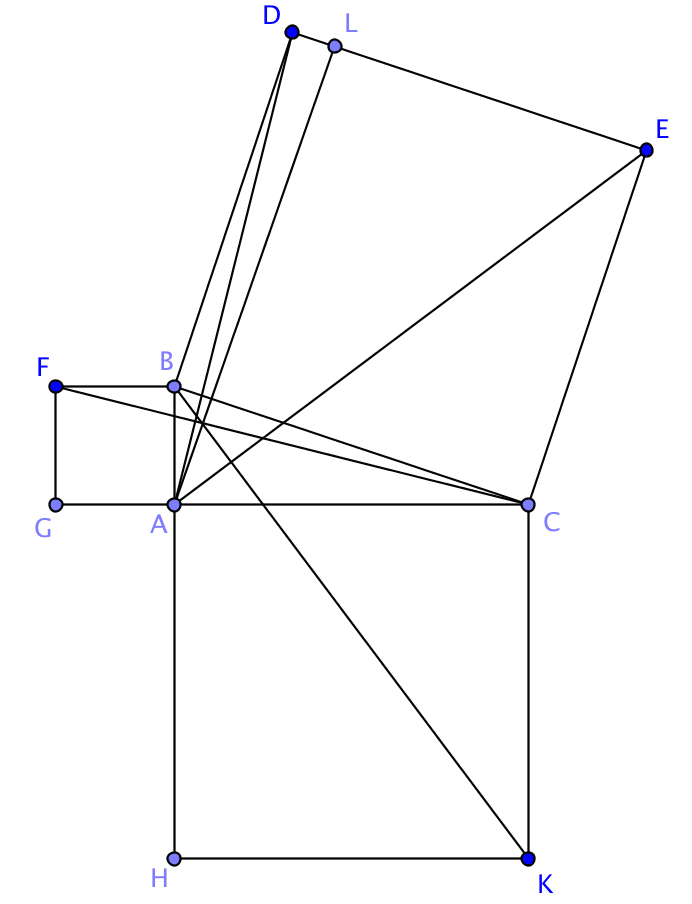
Prima di tutto osserviamo che i triangoli ABD e FBC sono isometrici. Inoltre, il rettangolo di lati BD e DL (L è piede della perpendicolare condotta da A al lato DE) ha area doppia dell'area del triangolo ABD, mentre il quadrato ABFG ha area doppia dell'area del triangolo FBC. Ne segue che il rettangolo di lati BD e DL ha area pari all'area del quadrato ABFG. Rifacendo lo stesso ragionamento sul quadrato ACHK si può concludere che il rettangolo di lati CE e EL ha area pari all'area del quadrato ACHK, da cui la conclusione.
Venendo ora ai due teoremi citati nel testo della domanda, sì, essi sono un'opportuna generalizzazione del teorema di Pitagora. La generalizzazione più evidente è data dal teorema del coseno, o teorema di Carnot, classico risultato di trigonometria piana. Dato il triangolo ABC come nella seguente figura
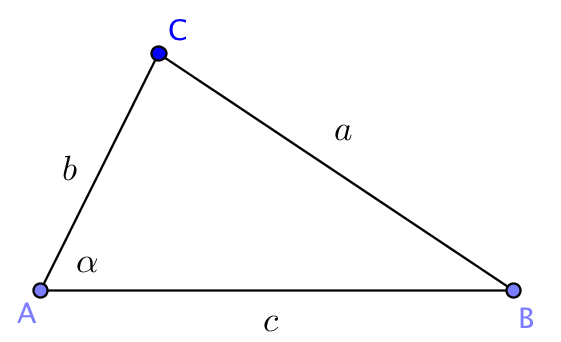
si ha la relazione a2=b2+c2-2bc cos α. Nel caso del triangolo rettangolo, con α angolo retto, il teorema di Carnot afferma che a2=b2+c2-2bc cos 90o=b2+c2, che fornisce il teorema di Pitagora.
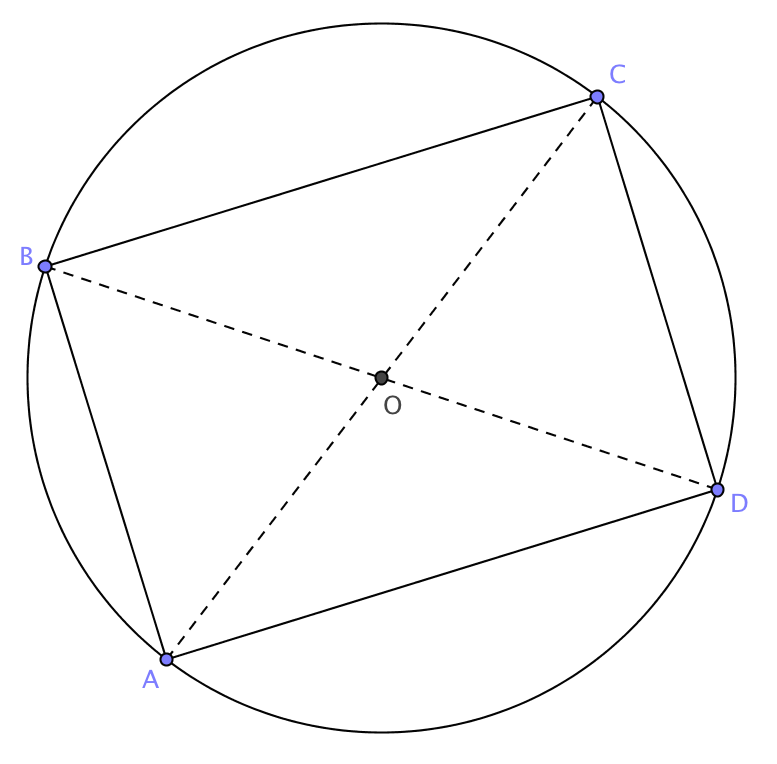
Più ampia discussione merita invece il teorema di Tolomeo, che spesso è trascurato dall'insegnamento della geometria piana. Viene attribuito all'astronomo greco Claudio Tolomeo vissuto nel primo secolo d.C. ed è oggi talvolta visto come teorema di trigonometria, in quanto una sua opportuna interpretazione in un caso particolare consente di dedurre le formula di addizione e sottrazione del seno; in effetti, Tolomeo stesso utilizzò questo risultato per la costruzione delle tavole dei seni. Riferendoci alla seguente figura
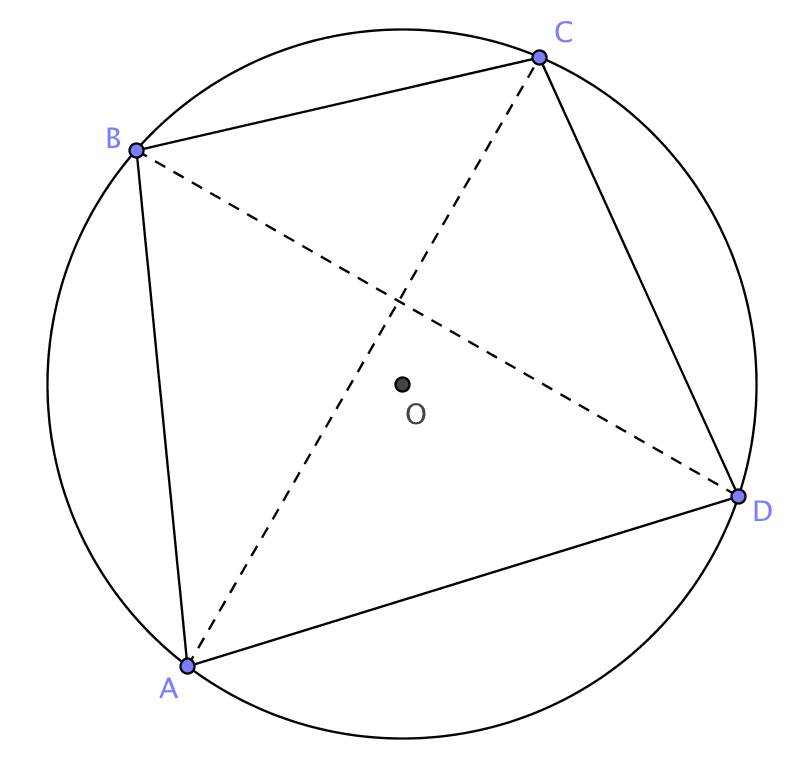
il teorema di Tolomeo afferma che se ABCD è un quadrilatero inscritto in un cerchio allora
AC • BD = AB • CD + AD • BC
ovvero, detto in altri termini, il rettangolo costruito con le diagonali equivale alla somma dei rettangoli costruiti cone le coppie dei lati opposti. Vediamo cosa diventa il teorema di Tolomeo se ABCD è un rettangolo. In figura abbiamo la seguente situazione:
e dunque la relazione di Tolomeo diventa AC2=AB2+AD2, che è il teorema di Pitagora.