Esistono tante dimostrazioni della divergenza della serie cosidetta armonica; quella più elementare si basa su un raggruppamento opportuno dei termini della serie stessa. Osserviamo infatti che data la serie
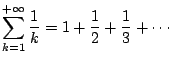
si ha anche
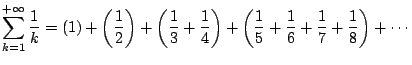
Ciascuno degli addendi tra parentesi risulta maggiore di 1/2 . Infatti
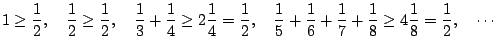
per cui la serie data diverge positivamente.
Vediamo di scrivere l’idea in termini matematici precisi; dimostriamo quindi per induzione su n che
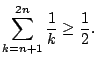
La tesi è banalmente verificata per n=1; supponiamo sia vera per n, allora si ha
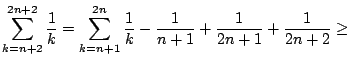
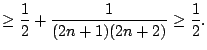
Ora è facile concludere; infatti denotando con
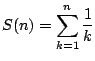
abbiamo dimostrato che, per ogni intero positivo n si ha
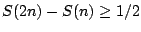 .
.
Ne segue che la successione S(n) non può essere una successione di Cauchy, per cui la serie armonica, per definizione, non converge, ma, essendo una serie a termini positivi, diverge positivamente.