Vorrei sapere come è possibile dimostrare matematicamente che i numeri Irrazionali sono densi nella retta dei numeri Reali e quindi tra due numeri Reali ci siano sempre sia un numero Razionale sia uno Irrazionale.

La dimostrazione discende dalle note proprietà di cardinalità degli insiemi numerici in questione.

Infatti ricordiamo che l’insieme dei numeri razionali Q è un insieme numerabile, ovvero ha la stessa cardinalità dell’insieme N dei numeri naturali. Invece R è un insieme molto più grande di Q, e infatti non è¨ numerabile, non ha la stessa cardinalità di Q, bensì ha la cosidetta potenza del continuo.

Premesso ciò, siano quindi dati due numeri reali x e y, con x<y. Vogliamo trovare un numero irrazionale (= non razionale) che stia tra x ed y.
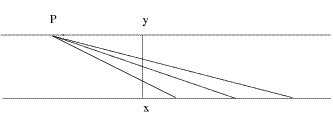
La seguente figura mostra come sia possibile stabilire una corrispondenza biunivoca tra l’intervallo aperto (x,y) e la semiretta aperta (0,+infinito):

Mettiamo infatti il segmento (x,y) verticalmente facendo coincidere x con l’origine 0 della semiretta reale, e proiettiamo da P i punti del segmento (x,y): otteniamo una corrispondenza 1 ad 1 con la semiretta aperta (0,+infinito).
Quello che abbiamo mostrato è dunque che il segmento aperto (x,y) ha la stessa cardinalità della semiretta (0,+infinito), che ha la stessa cardinalità dell’intera retta, ovvero R.
Ma allora l’insieme dei numeri tra x ed y non è numerabile; essendo invece in quantità numerabile l’insieme dei numeri razionali tra x ed y, ne segue che, nell’intervallo (x,y), esistono numeri che non sono razionali (dunque irrazionali).