Vorrei avere informazioni sul problema e sull’equazione di Keplero. In particolare vorrei avere le formule dell’angolo spazzato e del raggio in funzione del tempo.

Johannes Kepler
(Weil, Württemberg 1571 – Ratisbona 1630)

1 – Il problema di Keplero

Per inquadrare il problema che dovette affrontare Keplero, riportiamo di seguito un brano tratto dall’opera “Come io vedo il mondo” di A. Einstein (i corsivi sono nostri).

“Copernico aveva attirato l’attenzione delle menti più elette sul fatto che si poteva avere la nozione chiara del movimento apparente dei pianeti considerando questi moti come rivoluzioni intorno al sole supposto immobile. Se il moto di un pianeta era un moto circolare uniforme intorno al sole come centro, sarebbe stato relativamente facile stabilire quale doveva essere l’aspetto di quei movimenti visti dalla terra. Ma siccome esso si manifestava con fenomeni molto più complessi, il lavoro era assai più difficile. Bisognava determinare questi movimenti dapprima empiricamente secondo le osservazioni di Tycho Brahe sui pianeti. Soltanto in seguito si poteva pensare a trovare le leggi generali alle quali questi movimenti ubbidiscono.
Per capire quanto fosse difficile il compito di determinare il movimento reale di rotazione bisogna comprendere quel che segue. Non si vede mai dove si trova realmente un pianeta in un determinato momento; si vede soltanto in quale direzione esso è visto dalla Terra la quale descrive, essa stessa, una curva di natura sconosciuta intorno al Sole. Le difficoltà parevano dunque insormontabili.
Kepler trovò un mezzo per mettere ordine in questo caos. Prima di tutto egli riconobbe la necessità di determinare il movimento della Terra. Ciò sarebbe stato semplicemente impossibile se non ci fossero stati che il Sole, la Terra e le Stelle fisse senza alcun altro pianeta. Non si poteva in questo caso determinare null’altro che la variazione nel corso dell’anno della linea retta Terra-Sole (movimento apparente del Sole in rapporto alle Stelle fisse). Si poteva così conoscere che tutte queste direzioni si trovavano in rapporto alle Stelle fisse, almeno per quanto lo consentivano le imprecise osservazioni dell’epoca fatte senza telescopio. Bisognava anche determinare, allo stesso modo, come la linea Terra-Sole ruota intorno al Sole e si constatava che la velocità angolare di questo movimento si modifica regolarmente nel corso dell’anno. Ma questo non poteva ancora essere di molto aiuto poiché non si conosceva la variazione annuale della distanza Terra-Sole. Soltanto quando fossero conosciute le modifiche annuali di questa distanza sarebbe stato possibile tracciare la giusta traiettoria della Terra e determinare la legge.
Kepler trovò un mezzo ammirevole per uscire da questo dilemma. Anzitutto risultava dalle osservazioni solari che la velocità del percorso apparente del Sole sullo sfondo delle Stelle fisse era diversa nelle varie epoche dell’anno, ma che la velocità angolare di questo moto era sempre uguale nella stessa epoca dell’anno astronomico e di conseguenza la velocità di rotazione della linea Terra-Sole esaminata in rapporto alla medesima regione delle Stelle fisse, aveva sempre lo stesso valore. Si poteva dunque ammettere che l’orbita della Terra si richiudeva su se stessa e che la Terra la percorreva ogni anno nello stesso modo. Fatto per nulla evidente a priori. I seguaci di Copernico erano dunque certi che questo procedimento poteva applicarsi anche alle orbite degli altri pianeti.
Questo costituiva già un miglioramento. Ma come determinare la vera forma dell’orbita terrestre? Ammettiamo, in qualche punto del piano di quest’orbita, la presenza di una potente lanterna M: sappiamo che essa è fissa, che costituisce quindi per la determinazione dell’orbita terrestre una specie di punto fisso di triangolazione sul quale gli abitanti della Terra possono puntare in ogni epoca dell’anno. Ammettiamo inoltre che questa lanterna sia a maggior distanza dalla Terra. Ecco come, con l’aiuto di questa lanterna, si può determinare l’orbita terrestre.
Anzitutto c’è ogni anno un momento in cui la terra T si trova esattamente sulla linea che congiunge il Sole S alla lanterna M; se in questo momento si punta dalla Terra sulla lanterna, la direzione così ottenuta è anche la direzione SM (sole-lanterna).
Ammettiamo che questa direzione sia tracciata nel cielo. Prendiamo ora un’altra posizione della Terra in un altro momento. Poiché dalla Terra si può osservare egualmente bene il Sole e la lanterna, l’angolo T del triangolo STM è conosciuto. D’altra parte un’osservazione diretta del Sole dà la direzione ST e in precedenza si è determinato una volta per tutte la direzione SM sullo sfondo delle Stelle fisse. Si conosce anche l’angolo in S. Scegliendo a volontà una base SM, si può dunque tracciare sulla carta il triangolo STM. Si faccia questa costruzione parecchie volte durante l’anno e si otterrà ogni volta sulla carta un punto per la terra T in rapporto alla base SM definita una volta per tutte, corrispondente a una data stabilita. L’orbita terrestre sarebbe così determinata empiricamente, a parte, ben inteso, la sua dimensione assoluta.
Ma, voi direte, dove ha preso Kepler la lanterna M? I1 suo genio, aiutato in questo caso dalla natura benigna, gliel’ha fatta trovare. C’era, per esempio, il pianeta Marte, di cui si conosceva la rivoluzione annuale, cioè il tempo che questo pianeta impiega per fare un giro intorno al Sole. Può succedere che il Sole, la Terra e Marte a un dato momento si trovino esattamente in linea retta, e questa posizione di Marte si ripeta ogni volta in capo a uno, due, ecc. anni marziani, perché Marte percorre una traiettoria chiusa. In questo determinato momento, SM presenta sempre la stessa base, mentre la Terra si trova sempre in un punto diverso dalla sua orbita. Le osservazioni di Marte e del Sole, alle date in questione, forniscono di conseguenza un mezzo per determinare l’orbita terrestre vera, avendo il pianeta Marte, in quei momenti, la parte della lanterna fittizia di poco fa. È in questo momento che Kepler ha trovato la vera forma dell’orbita terrestre e le leggi che la governano: noialtri, venuti più tardi, dobbiamo onorarlo e ammirarlo per questo.
Una volta determinata empiricamente l’orbita terrestre, si conosceva in ogni momento, nella sua vera grandezza e direzione, la linea ST; allora non era più difficile per Kepler, in linea di principio, calcolare, secondo le osservazioni dei pianeti, le orbite e i movimenti di questi: un lavoro immenso, dato lo sviluppo delle matematiche in quell’epoca.
Restava ora la seconda parte, non meno difficile del lavoro che ha riempito la vita di Kepler. Le orbite erano conosciute empiricamente; ma, da questi risultati empirici, bisognava trarre le leggi. Bisognava anzitutto stabilire una ipotesi sulla natura matematica della curva e verificarla per mezzo di enormi calcoli, i cui dati erano già conosciuti; se il risultato non concordava, fare un’altra ipotesi e verificarla di nuovo. Dopo ricerche di cui si intuisce l’immensità, Kepler trovò un risultato concordante: l’orbita è un’ellisse di cui il Sole occupa uno dei fuochi. Egli trovò anche la legge della variazione della velocità sull’orbita, secondo la quale la linea Pianeta-Sole percorre superfici uguali in tempi uguali. Infine Kepler trovò anche che i quadrati dei tempi di rivoluzione sono proporzionali alle terze potenze degli assi maggiori dell’ellisse”.

2 – Le leggi di Keplero

Le intuizioni astronomiche di Keplero possono essere riassunte nelle sue tre grandi leggi (sebbene egli stesso non le chiamasse così; egli non le considerava tanto importanti quanto le sue scoperte musicali).

La prima legge afferma che l’orbita di ciascun pianeta attorno al Sole è un’ellisse e che il sole non si trova al centro ma in uno dei due fuochi di tale ellisse.

Se prendiamo una matita e un pezzo di corda di lunghezza 2a, tenendo le due estremità della corda unite assieme in un solo punto O, mettiamo la punta P della matita all’interno del laccio e la tiriamo in modo da mantenere tesa la corda; quindi, muovendo la matita sulla carta tracciamo un cerchio il cui raggio OP=a è lungo la metà della lunghezza della corda (il diametro AA‘, il più lungo segmento che congiunge due punti della circonferenza è uguale a 2a). Ma se noi mettiamo le due estremità della corda in due diversi punti, F e F’, e tracciamo una curva con la punta della matita (tenendo sempre tesa la corda), tale curva diventerà un’ellisse di cui i due punti F e F’ vengono chiamati fuochi.

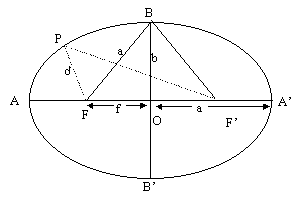
La linea passante per i due fuochi, prolungata fino a raggiungere l’ellisse (nei punti A e A’) è l’asse maggiore, il segmento più lungo che si può disegnare congiungente due punti dell’ellisse (e, come nel caso del diametro del cerchio, uguale alla lunghezza della corda, AA‘=2a). Il suo punto medio O è chiamato centro dell’ellisse e il segmento perpendicolare all’asse maggiore, passante per O, si chiama asse minore (il “diametro minore” dell’ellisse). La lunghezza AO=a (semiasse maggiore) e la simmetria e la costruzione originale richiedono che anche BF e BF‘ siano uguali ad a. La lunghezza BO viene definita come b (semiasse minore) mentre la lunghezza FO viene definita come f (distanza focale).

Dal teorema di Pitagora, a²=b²+f². Ovviamente il grado di “appiattimento” dell’ellisse (a-b)/a, cioè di quanto l’ellisse differisce dal cerchio, dipende da f o meglio dal rapporto f/a. Allo scopo di confrontare le forme di ellissi grandi e piccole (ellissi con valori diversi di a) è conveniente definire il rapporto f/a=e (eccentricità). Chiaramente se f e quindi e sono uguali a zero, F e F’ coincidono con O, e l’ellisse è una circonferenza; mentre se l’eccentricità e è uguale a 1 (f=a), l’ellisse sarà schiacciata e trasformata in un segmento lungo 2a. (E’ sufficiente conoscere soltanto due di queste quattro quantità, a, b, e, e f, per calcolare le altre due).

Così dalla prima legge di Keplero ne consegue che:

la distanza media di un pianeta dal Sole (che si trova in F) è a (quando il pianeta si trova in B o in B’)
la sua minima distanza (perielio) è a – f = a( 1 – e) (quando il pianeta si trova in A).
la sua massima distanza (afelio) è a + f = a(1+e) (quando il pianeta si trova in A’).

La distanza media è qui intesa come media aritmetica tra i due estremi. Inoltre, se si definisce t come il tempo trascorso dal momento in cui il pianeta è passato al perielio, espresso in trecentosessantesimi del periodo di rivoluzione attorno al Sole (periodo p espresso in anni) si ha:

(dove t, come argomento della funzione coseno deve essere espresso in gradi).

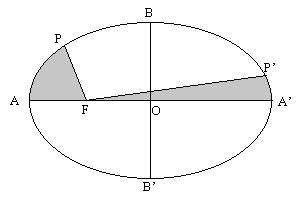
La seconda legge di Keplero è un po’ più astratta (vedi figura). Se un pianeta P è in movimento attorno al Sole, il quale per la prima legge occupa uno dei due fuochi F della sua orbita ellittica, possiamo immaginare il segmento che congiunge il pianeta con il Sole (PF) percorrere un’area dell’ellisse. La seconda legge afferma che due aree coperte da questo segmento in due periodi di tempo uguali, sono equivalenti (ad esempio le due aree più scure della figura). Affinché questo si verifichi il pianeta deve muoversi più rapidamente quando è più vicino al Sole (nel nostro esempio, il tratto di orbita tra P e A) e più lentamente quando è lontano (tra P’ e A’).

Così, sebbene la velocità del pianeta sia variabile, essa varia seguendo una precisa regola. Come Keplero sapeva, ci sono diversi tipi di velocità, ma ciascuno di essi è governato dalla stessa legge. La velocità lineare v (misurata ad esempio in chilometri al secondo) varia proporzionalmente come segue:

La velocità media è ora una media armonica tra i due estremi.

La velocità angolare , misurata prendendo come riferimento il Sole in F, varia nel seguente modo:

In termini di t,

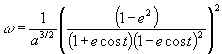
La terza legge di Keplero, chiamata talvolta legge armonica, afferma che il quadrato del periodo di rivoluzione del pianeta attorno al Sole, p, è esattamente proporzionale al cubo della sua distanza media dal Sole, a. Così:

Possiamo perciò sostituire a^3/2 con p nelle espressioni precedenti che diventano delle equazioni se p è espresso in anni e in numero di rivoluzioni all’anno o in gradi per trecentosessantesimi di anno:

Il valore medio è il quadrato della media armonica tra le radici degli estremi. In termini di t,

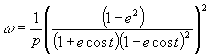
3 – Formulario

L’orbita di un corpo intorno ad una massa centrale è una conica, che si può esprimere in coordinate polari:

Dove r è il raggio vettore (il segmento FQ), theta è l’angolo (detto anche anomalia) formato dal raggio vettore con l’asse maggiore, p è l’ascissa al fuoco (il segmento NQ), che può essere espresso in funzione dei semiassi, ovvero p=b²/a.

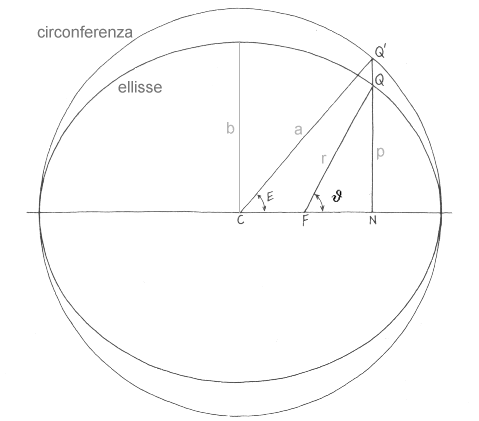
Venendo in particolare alle richieste del nostro lettore, ecco le espressioni differenziali della variazione di raggio ed anomalia rispetto al tempo:

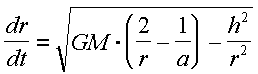
dove h in base alla seconda legge di Keplero è il doppio della velocità areolare, e cioè

Per quanto riguarda il legame tra theta ed r in funzione del tempo, dobbiamo dire che è molto più semplice ricavare t in funzione di theta partendo dalle due relazioni di Keplero, e poi invertire la relazione.

La prima relazione di Keplero lega l’anomalia vera theta all’anomalia eccentrica E:

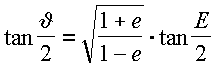
La seconda relazione di Keplero esprime il legame tra l’anomalia media M e quella eccentrica E, una volta nota l’eccentricità e. E’ una relazione trascendente di non facile soluzione.

Dato che l’anomalia media M è legata al periodo di rivoluzione T dalla seguente relazione

ed inoltre T si può esprimere con la terza legge di Keplero

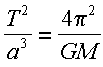
sostituendo e ricordando alcune proprietà dell’ellisse, giungiamo infine alla relazione

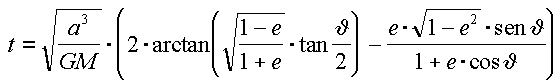
che ci fornisce il tempo t in funzione dell’anomalia vera theta, note l’eccentricità e e il semiasse maggiore a.
Volendo ricavare l’inversa, non è conveniente procedere per via analitica, è più semplice calcolare un certo numero di valori di t e leggere la tabella partendo da t per ricavare il corrispondente valore di theta.

4 – Orbite con Excel

Può essere divertente studiare come varia la forma dell’orbita e l’andamento della velocità variandone i parametri. Per questo scopo è stato realizzato un tutorial con il foglio di calcolo Excel. Al momento il lavoro è pesantemente incompleto, ciò nonostante, vi mettiamo a disposizione una versione preliminare.

Moto dei pianeti.zip (182 kB)

Bibliografia:

A. Leone, Il moto dei corpi celesti, Muzzio
M. Spiegel, Meccanica razionale, McGraw-Hill
A. Einstein, Come io vedo il mondo, Newton-Compton