Definizioni e
proprietà
Numeri primi
Nella risposta, vengono date per note le definizioni e
proprietà dei numeri primi, che possono essere comunque
reperite in altra risposta di “Chiedi all’esperto” ai due seguenti links:
Sui Numeri Primi – risposta di Luca
Fini
Sui Numeri Primi – risposta di Carlo
Consoli
Richiamiamo solo brevemente la definizione di numero
primo di Mersenne: un numero primo ottenibile come M(n)=2n-1
è detto numero primo di Mersenne.
Funzione MOD
La funzione MOD, resto o modulo,
è definita come il resto della divisione intera.
x mod y può essere calcolata in due modi:
- iterativamente, sottraendo y da x
fino ad ottenere un risultato minore di y - mediante la formula
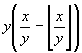 ove
ove 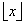
è la parte intera inferiore di x
Ad esempio:
20 mod 8 = 4
iterativamente: 20 – 8 = 12 – 8 = 4
con la formula: 8(2.5 – 2) = 4
Il test L-L
Il test di Lucas-Lehmer serve per testare la
primalità di un numero primo di Mersenne M(n)=2n-1.
M(n) è primo se e solo se s(n-2) mod M(n) = 0
ove s(n-2) è l’elemento n-2 della
successione esponenziale ricorsiva seguente:
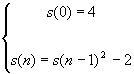
In altri termini, M(n) è primo se divisibile
per il termine s(n-2) della successione s(n).
Proviamo a calcolare i primi termini di s(n) applicandone
la definizione ricorsiva:
s(0)=4 è il valore iniziale
s(1) = 2s(0)-2 = 14 ad
ogni passaggio eleviamo 2 al valore precedente e
sottraiamo due
s(2) = 214-2 = 194
s(3) = 2194-2 = 37634
…e così via…
Con i termini appena calcolati possiamo testare se M(5)
= 31 è primo.
Applichiamo il test e calcoliamo
s(n-2) mod M(n) = s(5-2) mod M(5) = s(3) mod M(5)
= 37634 mod 31 = 0
M(5) è, quindi, primo.
Il problema del test L-L è che la successione s(n)
diverge con rapidità impressionante (esponenziale,
appunto).
Già il termine s(8) è un numero a 147 cifre
(si dice è dell’ordine di 10147):
s(8)=26216346504927851452605936955756303
921364787755952454591190600534955577383
123693501595628184893342699930798241866
4943276943901608919396607297585154
La fig. 1 illustra l’entità del fenomeno di
esplosione esponenziale
dell’ordine di grandezza degli elementi di s(n).
| S(n) | Ordine |
|
1 |
2 |
|
2 |
3 |
|
3 |
6 |
|
4 |
10 |
|
5 |
19 |
|
6 |
38 |
|
7 |
74 |
|
8 |
147 |
|
9 |
294 |
|
10 |
587 |
|
11 |
1172 |
|
12 |
2344 |
|
13 |
4686 |
|
14 |
9372 |
|
15 |
18743 |
|
16 |
37484 |
|
17 |
74967 |
|
18 |
149934 |
Fig.1:
Ordine di grandezza degli elementi di s(n)
s(18) è, quindi, un numero di quasi
centocinquantamila cifre !
Una comune calcolatrice scientifica non sarebbe in
grado di operare oltre il quarto elemento di s(n) ed
un moderno calcolatore dotato di software apposito inizia
a faticare intorno al ventesimo elemento (e questo è
anche il motivo per cui la tabella di Fig.1 si ferma ad s(18)).
Per questo motivo è stata ideata una versione
modificata della successione s(n) che mantenga le
stesse proprietà utili al test di primalità:
l’idea è di calcolare gli elementi di s(n) modulo
M(n)
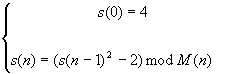
Nella versione modificata della successione s(n),
i coefficienti possono essere impiegati solo per testare
la primalità di M(n) ma, in compenso, il test è
molto più veloce.
Tra le altre cose, il test termina automaticamente
qualora s(n-2) = 0 perché
s(n-2) mod M(n) = 0 mod M(n) = 0
Nella versione modificaa, gli s(n) vengono
generati come sopra, salvo applicare il modulo M(n)
ad ogni passo.
Applichiamo la nuova definizione per calcolare, di
nuovo, il test di primalità di M(5):
s(0)=4 è il valore iniziale
s(1) = 2s(0)-2 = 14 mod
31 = 14 come sopra, ma mod 31
s(2) = 214-2 = 194 mod 31
= 8
s(3) = 2194-2 = 37634 mod
31 = 0 s(3) = 0
e 31 è un primo di Mersenne.
Una proprietà interessante dei primi di Mersenne è
che M(p) è primo se p è primo. Ciò
significa che, poiché 31 è primo, allora anche M(31)
deve esserlo.
Applichiamo il test per verificare la primalità di M(31)
= 231-1 = 2147483647 e
calcoliamo i 31-2 = 29 elementi di s(n),
nella versione modificata:
M(31) = 2147483647
s(0) = 4
14
194
37634
1416317954
669670838
1937259419
425413602
842014276
12692426
2044502122
1119438707
1190075270
1450757861
877666528
630853853
940321271
512995887
692931217
1883625615
1992425718
721929267
27220594
1570086542
1676390412
1159251674
211987665
1181536708
65536
s(29) = 0
E, quindi, M(31) è primo.
Si osservi come il numero di cifre degli elementi s(i)
non superi mai il numero di cifre di M(n): questa
proprietà è sempre vera per definizione di modulo.
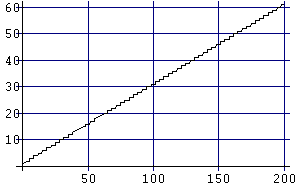
Fig.2: Ordine di
grandezza degli elementi di s(n) modificata
In ascissa è il numero n, in ordinata
l’ordine massimo dei termini s(n). La figura
2 illustra, quindi, un andamento quasi-lineare
dell’ordine di grandezza dei termini al crescere di n.
Ciò significa che possiamo tranquillamente procedere
al test di primalità per M(50) ed attenderci
calcoli che coinvolgano un numero di cifre pari, al più,
a quelle di M(50) stesso, circa 18.
Alcune considerazioni
conclusive
Per dare l’idea dei benefici apportati dal test
di Lucas- Lehmer, nella versione modificata, un comune PC
con processore K6-2 a 333Mhz e Mathematica è in
grado di testare M(200), un numero di 60 cifre (il
fondo-scala della figura 2), in meno di 10 secondi.
Testare la primalità di un numero vuol dire
verificarne la non divisibilità per ciascun numero della
serie dei numeri primi che lo precedono ed il Teorema di
Numeri primi asserisce che il numero dei numeri primi
minori o uguali n è circa n/log n. Ciò
implica che dovremmo eseguire circa 1058
divisioni per eseguire il test di primalità di M(200).
Supponendo di avere un supercomputer in grado di
eseguire un miliardo di divisioni al secondo impiegando
numeri a 60 cifre (roba da fantascienza, almeno ad oggi),
impiegheremmo 1041 anni: si parla di miliardi
di miliardi di miliardi di miliardi di anni.
Il test di Lucas- Lehmer consente, quindi, di
abbreviare notevolmente i tempi di verifica di primalità
dei primi di Mersenne, svicolando l’intrattabilità
del problema della fattorizzazione.
La figura 2 illustra l’ordine di grandezza degli
elementi di s(n) modificata.